Set Kuramının kökeni 1873'de Cantor'un "gerçek çizginin sayılamazlığını" tanıtlaması üzerine dayandırılır ("the uncountability of the real line").

O güne dek hiç kimse "sonsuzlukların değişik büyüklüklerde gelmesi olanağını" tasarlamamıştı ("the possibility that infinities come in different sizes").

Gerçekte sonsuz, ya da daha tam olarak "edimsel sonsuz" matematiksel bir nesne değil, çünkü bir nicelik değil ama bir niteliktir. Cantor bir niteliği nicelik yapma girişiminde bulunan ilk matematikçidir, gerçi sonlu-ötesi sayılarının kendileri sonsuzluk ile hiçbir ilgileri olmayan sonlu nicelikler olsalar da. Leibniz'ün ayrışımlı kalkülüsü sonsuzu kullanmaz ve "matematiksel sonsuz" Gauss'un deyimi ile en iyisinden "bir konuşma tarzı" olarak görünür.


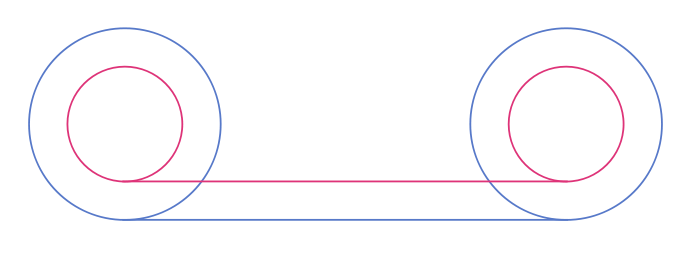
Aristoteles'e yüklenen tekerlek paradoksu. (Bu paradoksu Galileo da ele alır.)
Ayrı çaplar ile iki eşözekli daireden oluşan bir tekerleğin büyük çemberi ve küçük çemberi üzerindeki noktalar arasında bire-bir (1:1) bir çakışma olduğu ve bu nedenle iki ayrı dairenin aynı uzunluğu geçtiği düşünülür. Buna göre ayrı çapları olan iki dairenin aynı çevre uzunluğunu taşımaları gerektiği paradoksu doğar. Yanıltı iki daire üzerindeki noktaların bire-bir karşılık düştükleri sanısından doğar. Bir daire üzerindeki noktaları saymak ise ancak Cantor'un başarabileceği bir büyücülüktür.

Modern "matematiğin" bir açıklaması şöyledir: herhangi bir uzunluktaki bir çizgi dilimi üzerindeki, ya da sonsuz bir çizgi ya da bir düzlem üzerindeki, üç-boyutlu bir uzay ya da sonsuz boyutlu bir Euklides-uzayındaki noktaların "kardinaliteleri" tümü de aynıdır: c, ya da cardinality of the continuum. Buna göre bunlardan herhangi birinin noktaları başka herhangi birinin noktaları ile bire-bir karşılık düşme içine koyulabilir.

Sormamız gereken şey "cardinality"nin ne olduğudur. Soralım.

Bir yanıt şudur (Wikipedia): "Bir setin kardinalitesi "setin öğelerinin sayısının" bir ölçüsüdür. Örneğin A = {2, 4, 6} kümesi üç öğe kapsar ve öyleyse kardinalitesi 3'tür. Başka bir deyişle, sayılabilir öğeler her durumda sonludur.
Biraz daha izleyelim: Kardinaliteye iki yaklaşım vardır, denir. Biri bijeksiyonları (bire-bir örtüşmeleri) ve injeksiyonları (bire-bir fonksiyonları) kullanarak setleri doğrudan karşılaştıran, ve ikincisi kardinal sayıları kullanan yaklaşım. Bijeksiyonlar ve injeksiyonlar sonludur. "Kardinal sayıların" ne olduğunu sormamız gerekir. Soralım.

Yanıt: Bir A setinin kardinalitesi (= büyüklüğü) genellikle |A| ile belirtilir, ki saltık değer ile aynı notasyondur. Ya da başka belirtme yolları kullanılabilir, örneğin card(A) gibi. Kardinal sayılar bir setin kardinalite ya da "büyüklüğünü/size" ölçmek için kullanılır. Sonlu bir kümenin kardinalitesi setteki öğelerin sayısını gösteren bir doğal sayıdır. Sonsuz setlerin büyüklüklerini betimlemek için sonlu-ötesi kardinal sayılar kullanılır. Sonlu-ötesi (trans-finite) kardinal sayılar nedir? Soralım.

Yanıt: Sonlu-ötesi sayılar tüm sonlu sayılardan daha büyük olmaları anlamında "sonsuz" olan sayılardır, ve saltık olarak sonsuz olmaları zorunlu değildir. (Wikipedia)

Wikipedia ya da başka herhangi bir kaynak bu anlatım biçimini değiştirebilir. Ama ne olursa olsun "trans-finite" sayıların "saltık olarak sonsuz" olduklarını, kısaca "sonsuz" olduklarını ileri sürmeyecektir. Sonlu-ötesinin kendisinin sonlu olması gerçekte yalın olarak "öte" kavramının kendisinden gelir, çünkü "öte" birşeyi sınırlarken, kendisi o birşey tarafından sınırlanır.

Bir çizgi dilimi, bir yüzey parçası vb. üzerindeki noktaların sayılması düşüncesi bir kavram bozukluğu, gerçekte us-yarılması dediğimiz şeydir. Küçük tekerleğin dairesi üzerindeki noktaların büyük tekerleğin dairesi üzerindeki noktalara bire-bir karşılık düştüğü "düşüncesi" gerçekte bir düşünce değil ama bir rahatsızlık belirtisidir.

Sonlu-ötesi "sonsuz" sayıların esin kaynağı her belirli niceliğin, eş deyişle her nicenin sonsuza bölünebilir olmasıdır. Bu bölünebilirlikten çıkarak birbirlerine eşit olmayan sonsuzların "olduğu" vargısına ulaşmak belirli nicelikleri sonsuz nicelikler yapmak olarak görünür.

Tepe

Forget everything you know about numbers.

In fact, forget you even know what a number is.

This is where mathematics starts.

Instead of math with numbers, we will now think about math with "things".

"Set Theory is the mathematical science of the infinite." (Stanford Encyclopedia of Philosophy) Set Kuramı, her "kuram" gibi, bilgi değildir. Örneğin görelilik "kuramları," quantum "kuramları" gibi. Us, salt sezgisel olarak bile olsa, henüz ussal olduğu tanıtlanmamış olan kurgulara bilim adını vermez. Gereken şey doğrulama değil ama tanıtlamadır, çünkü görgül doğrulama salt bir görüngünün aklaması iken, kuramın kendini tanıtlaması ussal-kavramsal yapısının kendi kendisini doğrulamasıdır. Görüngü kuramı belirlemez, tersine kuram görüngüyü belirler. Deneyim kavram üretmez, ama kavram deneyimi belirler. Ama yukarıdaki tanımda asıl çarpık olan şey set kuramının "sonsuzun" matematiksel bilimi olduğu biçimindeki düşüncesiz bildirimdir. "Sonsuz" matematiğin nesnesi olabilecek bir nicelik değildir. "Sonsuz" bir niteliktir.

"As sets are fundamental objects that can be used to define all other concepts in mathematics, they are not defined in terms of more fundamental concepts. Rather, sets are introduced either informally, and are understood as something self-evident, or, as is now standard in modern mathematics, axiomatically, and their properties are postulated by the appropriate formal axioms." (Stanford Encyclopedia of Philosophy)

Gerçekte, kümeler "nesneler" olmakla temel olma karakterini daha baştan yitirirler çünkü nesnenin kendisinin mantıksal öncülleri vardır. Kümeler matematikteki başka kavramları tanımlamak yerine, tersine kendileri daha temel nicelik kavramı tarafından tanımlanırlar. Kümeler hiç kuşkusuz kendiliğinden-açık şeylerdir, çünkü birer algı nesnesidirler; belitsel (axiomatic) olmaktan öylesine uzaktırlar ki, "appropriate formal axioms" denilen şeyler birer belit olmaya uygun değildir.

Tepe

A set is just a collection of things with some common property.

NOKTADAN ÇİZGİ
When we collect ALL points that share a property we can end up with a line, a surface or other interesting thing.



(Note: the points are drawn as dots so you can see them, but they really should have no size at all)

Noktalar boyutsuz oldukları, uzayın saltık olumsuzlaması oldukları için, ardarda dizilen sonsuz sayıda nokta ancak bir nokta eder.

ÇİZGİDEN YÜZEY
Example: A Circle is: "the set of all points on a plane that are a fixed distance from a central point".

So, just a few points start to look like a circle, but when we collect ALL the points, we will actually have a circle.

Tepe

Frege, Grundlagen der Arithmetik

§ 85 Kısa bir süre önce G. Cantor dikkate değer bir çalışmada sonsuz sayıları getirmiştir. Genel olarak yalnızca sonlu sayıların edimsel olarak geçerli sayılması gerektiği görüşünü değerlendirmede onunla baştan sona anlışıyorum. Ne bunlar, ne kesirler, ne de negatif kesirsiz ve karmaşık sayılar duyusal olarak algılanabilir ve uzaysaldır; ve eğer duyular üzerine etkide bulunana ya da en azından duyu-algılarını yakın ya da uzak sonuçlar olarak getirebilen etkiler taşıyana edimsel denirse, o zaman hiç kuşkuz bu sayılardan hiç biri edimsel değildir. Ama hiçbir biçimde böyle algılara kuramlarımız için tanıtlama zemini olarak gereksinim duymayız. Mantıksal olarak karşı çıkılamaz bir yolda getirilen bir ad ya da bir im araştırmalarımızda hiç duraksamadan kullanılabilir, ve böylece ∞1 sayımız iki ya da üç sayısı gibi aklanır.

§ 85 Vor Kurzem hat G. Cantor in einer bemerkenswerthen Schrift*) unendliche Anzahlen eingeführt. Ich stimme ihm durchaus in der Würdigung der Ansicht bei, welche überhaupt nur die endlichen Anzahlen als wirklich gelten lassen will. Sinnlich wahrnehmbar und räumlich sind weder diese noch die Brüche, noch die negativen, irrationalen und complexen Zahlen; und wenn man wirklich nennt, was auf die Sinne wirkt, oder was wenigstens Wirkungen hat, die Sinneswahrnehmungen zur nähern oder entferntern Folge haben können, so ist freilich keine dieser Zahlen wirklich. Aber wir brauchen auch solche Wahrnehmungen gar nicht als Beweisgründe für unsere Lehrsätze. Einen Namen oder ein Zeichen, das logisch einwurfsfrei eingeführt ist, können wir in unsern Untersuchungen ohne Scheu gebrauchen, und so ist unsere Anzahl ∞1 so gerechtfertigt wie die Zwei oder die Drei.

Tepe

Lorem ipsum .

Tepe

Frege, Grundlagen der Arithmetik

§ 85 Kısa bir süre önce G. Cantor dikkate değer bir çalışmada sonsuz sayıları getirmiştir. Genel olarak yalnızca sonlu sayıların edimsel olarak geçerli sayılması gerektiği görüşünü değerlendirmede onunla baştan sona anlışıyorum. Ne bunlar, ne kesirler, ne de negatif kesirsiz ve karmaşık sayılar duyusal olarak algılanabilir ve uzaysaldır; ve eğer duyular üzerine etkide bulunana ya da en azından duyu-algılarını yakın ya da uzak sonuçlar olarak getirebilen etkiler taşıyana edimsel denirse, o zaman hiç kuşkuz bu sayılardan hiç biri edimsel değildir. Ama hiçbir biçimde böyle algılara kuramlarımız için tanıtlama zemini olarak gereksinim duymayız. Mantıksal olarak karşı çıkılamaz bir yolda getirilen bir ad ya da bir im araştırmalarımızda hiç duraksamadan kullanılabilir, ve böylece ∞1 sayımız iki ya da üç sayısı gibi aklanır.

§ 85 Vor Kurzem hat G. Cantor in einer bemerkenswerthen Schrift*) unendliche Anzahlen eingeführt. Ich stimme ihm durchaus in der Würdigung der Ansicht bei, welche überhaupt nur die endlichen Anzahlen als wirklich gelten lassen will. Sinnlich wahrnehmbar und räumlich sind weder diese noch die Brüche, noch die negativen, irrationalen und complexen Zahlen; und wenn man wirklich nennt, was auf die Sinne wirkt, oder was wenigstens Wirkungen hat, die Sinneswahrnehmungen zur nähern oder entferntern Folge haben können, so ist freilich keine dieser Zahlen wirklich. Aber wir brauchen auch solche Wahrnehmungen gar nicht als Beweisgründe für unsere Lehrsätze. Einen Namen oder ein Zeichen, das logisch einwurfsfrei eingeführt ist, können wir in unsern Untersuchungen ohne Scheu gebrauchen, und so ist unsere Anzahl ∞1 so gerechtfertigt wie die Zwei oder die Drei.

Tepe

MILL
Cognition is receptive. It is not formative or constitutive of its objects. (?)

KANT
Up to now it has been assumed that all our cognition must conform to the objects; but all attempts to find out something about them a priori through concepts that would extend our cognition have, on this presupposition, come to nothing. Hence let us try whether we do not get farther with the problems of metaphysics by assuming that the objects must conform to our cognition. . . .


This attempt is Kant’s ‘‘Copernican revolution’’:

If intuition [sensory cognition of objects] has to conform to the constitution of objects, then I do not see how we can know anything of them a priori; but if the object (as an object of the senses) conforms to the constitution of our faculty of intuition, then I can very well represent this possibility to myself.2

Tepe

Leila Haaparanta The Development of Modern Logic 2009

Frege’s Foundations of Arithmetic (Die Grundlagen der Arithmetik, 1884) added, after an elaborate criticism of earlier and contemporary views on the concept of number and on arithmetical statements, a “purely logical” (today dubbed “logicist”) notion of whole number by defining the number n as the extension of the concept “equinumerous to the concept Fn,” where Fn is a model concept with exactly n objects falling under it, and of a purely logical nature guaranteed by starting with F0 = ¬-x = x and constructing Fn+1 recursively from Fn. Frege’s attainment of this notion is somewhat curious because immediately before that he had described and analyzed an attempt at defining number by abstraction directly from equinumerous concepts, but had repudiated this attempt because of difficulties that he considered insurmountable, so that he decided on the explicit definition just given. Grundlagen also introduced important logical distinctions like that of first-order and second-order concepts, with existence and number predicates as examples of the latter.

Tepe

Kant'a göre matematiksel önermeler sentetik a prirori karakter gösterir.

Tepe