
David Hilbert /
Sonsuz Üzerine
/ On the Infinite
(1925)
Çeviri, Çözümlemeler ve Notlar: Aziz Yardımlı |

SONSUZ ÜZERİNE — David Hilbert
Bu deneme (1925)
Paul Benacerraf ve
Hilary Putnam
tarafından yayıma hazırlanan
Philosophy of Mathematics’te
bulunuyor.
|
ON THE INFINITE — David Hilbert
Delivered June 4, 1925, before a congress of the Westphalian Mathematical
Society in Munster, in honor of Karl Weierstrass.
Translated
by Erna Putnam and Gerald J. Massey from Mathematische Annalen (Berlin) no. 95 (1925), pp. 161-90. Sprinter
verlag. |
|

‘‘Bu önemsiz notalarda oyalanmak sıkıcıdır,
ama çocuklaşma zamanları da
vardır.’’
Pascal (1658), ‘‘Geometrik Anlık Üzerine‘‘
(‘‘De l’esprit de géométrique’’). |


—
Weierstrass ‘‘sonsuz küçüklük çevresindeki tüm karışık tasarımları uzaklaştırdı. |
| 1. Derine
işleyen eleştirisinin bir sonucu olarak, Weierstrass matematiksel analiz
için sağlam bir temel sağlamıştır. Birçok kavramı, özel olarak minimum,
fonksiyon ve ayrımsal bölüm (differential quotient) kavramlarını durulaştırarak, sonsuz
küçüklük kalkülüsünde henüz bulunan kusurları ortadan kaldırdı, sonsuz küçüklük
çevresindeki tüm karışık tasarımları uzaklaştırdı, ve böylelikle
o kavramdan doğan güçlükleri çözdü. Eğer bugün analizde kesirsiz sayı
ve sınır kavramları üzerine dayalı olan tümdengelimli yöntemleri kullanmada
tam anlaşma ve pekinlik var ise, ve eğer ayrımsal ve tümlev denklemler kuramının
en karmaşık sorularında, değişik sınır türlerinin en ustaca ve değişik bileşimlerinin
kullanımına karşın, gene de elde edilen sonuçlar açısından görüş birliği
var ise, o zaman işlerin bu mutlu durumu birincil olarak Weierstrass’ın bilimsel
çalışmasından ötürüdür. |
1. As a result of his penetrating critique, Weierstrass has provided a
solid foundation for mathematical analysis. By elucidating many notions,
in particular those of minimum, function, and differential quotient, he
removed the defects which were still found in the infinitesimal calculus,
rid it of all confused notions about the infinitesimal, and thereby completely
resolved the difficulties which stem from that concept. If in analysis today
there is complete agreement and certitude in employing the deductive methods
which are based on the concepts of irrational number and limit, and if in
even the most complex questions of the theory of differential and integral
equations, notwithstanding the use of the most ingenious and varied combinations
of the different kinds of limits, there nevertheless is unanimity with respect
to the results obtained, then this happy state of affairs is due primarily
to Weierstrass’s scientific work. |
2. Ve gene
de Weierstrass’ın sonsuz küçüklük kalkülüsü için sağladığı temele karşın,
analizin temelleri konusundaki tartışmalar sürmektedir. |
2. And yet
in spite of the foundation Weierstrass has provided for the infinitesimal
calculus, disputes about the foundations of analysis still go on. |
3. Bu güçlükler
sona ermemiş çünkü matematikte kullanıldığı biçimiyle sonsuz kavramının anlamı hiçbir zaman tam
olarak durulaştırılmamıştır. Weierstrass’ın analizi gerçekten
de sonsuz büyüğü ve sonsuz küçüğü onlar üzerine bildirimleri sonlu büyüklükler
arasındaki ilişkiler [üzerine bildirimlere] indirgeyerek ortadan kaldırdı.
Gene de sonsuz henüz sonsuz gerçek sayıları tanımlayan sayısal dizide
ve hep birden varolan tamamlanmış bir bütünlük olarak düşünülen gerçek
sayı dizgesinin kavramında kendini gösterir. |
3. These disputes
have not terminated because the meaning of the infinite, as that
concept is used in mathematics, has never been completely clarified.
Weierstrass’s analysis did indeed eliminate the infinitely large and the
infinitely small by reducing statements about them to [statements about]
relations between finite magnitudes. Nevertheless the infinite still appears
in the infinite numerical series which defines the real numbers and in
the concept of the real number system which is thought of as a completed
totality existing all at once. |
—
‘‘Sonsuz’’ Kavramı Matematikte "Hiçbir Zaman" Tam
Olarak Durulaştırılmamıştır
Hilbert’in
sözlerini kendisinin istediği gibi matematiksel sağınlık içinde
almalıyız. ‘Hiçbir zaman’ tam olarak ‘hiçbir zaman’ demektir. Hilbert
onun için anlaşılır olmayan bir kavramın başkaları için de anlaşılır olmadığını, yani kendisinin bilmediğinin başka hiç kimse için anlaşılır olmadığını düşünür. Bu "kategori eksikliği problemi" diyebileceğimiz bir durumdur, ve bir bilinç bir kategoriden yoksun olduğu zaman yoksunluğunun bilincinde olmaması olgusundan doğar.
Hilbert Doğal usunu dinleyerek Kavramın evrenselliği için isteminde
haklıdır, ama evrenselliğini istediği şeyin doğasını biliyor görümez.
Hilbert için bir bilmece olan problemi çözenler vardır. Aslında çözüm çok
eskilere gider. Aristoteles’in sonsuzun bir Nicelik değil ama bir Nitelik olduğu bildirimi matematikte kullanılan "sonsuzluk" tasarımının, bir sayı olduğu
düzeye dek, gerçekte ancak ve ancak sonlu olabileceği sonucuna
götürür. Bu "sonlu sonsuz" Hegel'in "kötü sonsuz" dediği şeydir. Gene de Hilbert problemin üzerine felsefesiz gitmede, aslında bilimsel ussal düşünce pahasına gitmede diretir. |
4. Analiz için temelinde, Weierstrass sonsuzun kavramını içeren mantıksal
tümdengelim biçimlerini koşulsuzca kabul etti ve yineleyerek kullandı —
örneğin belli bir özelliği olan tüm gerçek sayılar ele alındığı zaman
ya da belli bir özelliği olan gerçek sayıların varolduğu ileri sürüldüğü
zaman olduğu gibi.
|
4. In his foundation for analysis, Weierstrass accepted unreservedly and
used repeatedly those forms of logical deduction in which the concept of
the infinite comes into play, as when one treats of all real numbers
with a certain property or when one argues that there exist real
numbers with a certain property. |
5. Bu
nedenle sonsuz Weierstrass’ın kuramında bir başka kılık altında yeniden ortaya
çıkabilir ve böylece onun eleştirisi tarafından dayatılan sağınlıktan kaçabilir.
Öyleyse kökten çözmemiz gereken şey az önce belirtilen anlamda sonsuzun
problemidir. Tıpkı sonsuz küçüklük kalkülüsünün sınır süreçlerinde sonsuz
büyük ve sonsuz küçük anlamında sonsuzun
yalnızca bir eğretileme olarak çıkmış olması gibi, onun
tümdengelimli yöntemlerde kullanımını imleyen sonsuz
bir büyüklük anlamında sonsuzun bir yanılsama olduğunu da
anlamalıyız. Tıpkı sonsuz küçüklük ile işlemlerin tam olarak aynı sonucu
veren ve tam olarak aynı zarif biçimsel ilişkilere götüren sonlu ile değiştirilmesi
gibi, genel olarak sonsuz üzerine dayanan tümdengelimli yöntemler de tam
olarak aynı sonuçları veren, e.d., aynı tanıtlama zincirlerini ve formül
ve teoremlere ulaşmanın aynı yöntemlerini olanaklı kılan sonlu yordamlar
ile değiştirilmelidir.
|
5. Hence the infinite can reappear in another guise in Weierstrass’s theory
and thus escape the precision imposed by his critique. It is, therefore, the problem of the infinite in the sense just indicated which we
need to resolve once and for all. Just as in the limit processes of the
infinitesimal calculus, the infinite in the sense of the infinitely large
and the infinitely small proved to be merely a figure of speech,
so too we must realize that the infinite in the sense of an infinite totality,
where we still find it used in deductive methods, is an illusion. Just
as operations with the infinitely small were replaced by operations with
the finite which yielded exactly the same results and led to exactly the
same elegant formal relationships, so in general must deductive methods
based on the infinite be replaced by finite procedures which yield exactly
the same results; i.e., which make possible the same chains of proofs and
the same methods of getting formulas and theorems. |
—
‘‘Sonsuz’’ Bir Eğretilemedir |
| 6. Kuramımın hedefi en temel anlamda matematiksel
yöntemlerin pekinliğini sağlamaktır. Bu giderek sonsuz küçüklük kalkülüsünün
bunalımlı dönemi sırasında bile başarılmış olmayan bir görevdir. Bu kuram
böylece Weierstrass’ın analiz için kendi temeli yoluyla başarmayı umduğunu
ve yerine getirme yönünde zorunlu ve önemli bir adımi atmış olduğu şeyi
tamamlamalıdır. |
6. The goal of my theory is to establish once and for all the certitude
of mathematical methods. This is a task which was not accomplished even
during the critical period of the infinitesimal calculus. This theory
should thus complete what Weierstrass hoped to achieve by his foundation
for analysis and toward the accomplishment of which he has taken a necessary
and important step. |
| 7. Ama sonsuzun kavramını durulaştırma konusuyla ilgili çok daha genel bir
bakış açısı vardır. Dikkatli bir okur matematik yazınının kaynaklarını sonsuzda
bulan ahmaklık ve saçmalıklarla dolup
taştığını bulacaktır. Örneğin, sanki sınırlayıcı bir koşul imiş gibi, sağın
matematikte yalnızca sonlu bir sayıda tümdengelimin kabul edilebilir
olduğunda direten yazarlarla karşılaşırız — sanki herhangi biri çıkıp bunların
sonsuz bir sayısını üretmeyi başarmış gibi. |
7. But a still more general perspective is relevant for clarifying the
concept of the infinite. A careful reader will find that the literature
of mathematics is glutted with inanities and absurdities which have had
their source in the infinite. For example, we find writers insisting,
as though it were a restrictive condition, that in rigorous mathematics
only a finite number of deductions are admissible in a proof as if
someone had succeeded in making an infinite number of them. |
| 8. Yine çoktandır terkedildiklerini sandığımız eski karşıçıkışlar değişik
biçimlerde yeniden ortaya çıkarlar. Örneğin yakınlarda görünen biri şudur:
Gerçi bir kavramı herhangi bir risk olmaksızın, e.d. çelişkiler yaratmaksızın
getirmek olanaklı olabilse de, ve üstelik getirilmesinin hiçbir çelişkinin
doğmasına neden olmadığı tanıtlanabilse bile, gene de kavramın getirilmesi
böylelikle aklanmış olmaz. Bu tam olarak bir zamanlar karmaşık-imgesel
sayılara karşı getirilen şu aynı karşıçıkış değil midir: ‘‘Doğru, kullanımları
çelişkilere götürmez; ama gene de getirilmeleri yersizdir, çünkü imgesel
büyüklükler yoktur’’? Eğer, tanıtlayıcı tutarlıktan ayrı olarak, bir ölçmenin
aklanması sorusu herhangi bir anlam taşıyacaksa, ancak ölçmenin birlikte
yer alan başarının eşliğinde olup
olmadığını saptamaktan oluşabilir. Böyle başarı gerçekte özseldir, çünkü
başka yerlerde olduğu gibi matematikte de başarı
en yüksek mahkemedir ki kararlarına herkes boyun eğer. |
8. Also old objections which we supposed long abandoned still reappear in different
forms. For example, the following recently appeared: Although it may
be possible to introduce a concept without risk, i.e., without getting contradictions,
and even though one can prove that its introduction causes no contradictions
to arise, still the introduction of the concept is not thereby justified.
Is not this exactly the same objection which was once brought against complex-imaginary
numbers when it was said: ‘‘True, their use doesn’t lead to contradictions.
Nevertheless their introduction is unwarranted, for imaginary magnitudes
do not exist.’’? If, apart from proving consistency, the question of
the justification of a measure is to have any meaning, it can consist only
in ascertaining whether the measure is accompanied by commensurate success.
Such success is in fact essential, for in mathematics as elsewhere success
is the supreme court to whose decisions everyone submits. |
—
Matematik De Pragmatik Bir Bilimdir!
Einstein’ın geometrinin fizikselleştirilmesi istemine koşut olarak, bu
Hilbert’in matematiğin fizikselleştirilmesi istemini anlatım yollarından
biridir. Matematikte de böyle pragmatizme alışmamız gerekir. Bir sonraki
paragraf tümdengelimli bildirimlerin çelişkilere götürdükleri, buna karşı
yalnızca "olguların" çelişkiden bağışık olduklarını
belirtir. Hilbert’in matematiğe yaklaşımının felsefi temelleri tamamlanmıştır
ve bütünüyle açıkta yatar, ve bunlar bir çıkarsama girişimi ile ortaya serilmeyi
gereksizleştirir.
“The only infallible criterion of wisdom to vulgar minds — success.”
— Edmund Burke
|
| 9. Kimi insanların hayaletler görmesi gibi, bir başka yazar ne olursa
olsun hiçbir bildirimin yapılmadığı yerde bile çelişkiler görüyor gibi
görünür, örneğin ‘‘tutarlı olarak işlev görmesini’’ özel bir sayıltı olarak
aldığı somut duyum dünyasında. Benim
kendim her zaman yalnızca bildirimlerin, ve tümdengelimler yoluyla bildirimlere
götürdükleri ölçüde hipotezlerin birbirleri ile çelişebileceklerini kabul
etmişimdir. Olguların ve olayların kendilerinin
çelişki içinde olabilecekleri görüşü bana dikkatsiz düşünmenin
birincil bir örneği olarak görünür. |
9. As some people see ghosts, another writer seems to see contradictions
even where no statements whatsoever have been made, viz., in the concrete
world of sensation, the ‘‘consistent functioning’’ of which he takes as
special assumption. I myself have always supposed that only statements,
and hypotheses insofar as they lead through deductions to statements, could
contradict one another. The view that facts and events could themselves
be in contradiction seems to me to be a prime example of careless thinking. |
— Hilbert İçin Çelişki Görgül / Olgusal Değil Ama Salt Düşünseldir |
| 10. Yukarıdaki gözlemlerin biricik amacı sonsuzun doğasının belirleyici
durulaştırmasının, yalnızca özelleşmiş bilimsel ilgilerin alanına ait
olmak yerine, insan anlağının kendisinin vakarı için gerekli olduğu
olgusunu göstermektir. |
10. The foregoing remarks are intended only to establish the fact that the
definitive clarification of the nature of the infinite, instead of
pertaining just to the sphere of specialized scientific interests, is needed
for the dignity of the human intellect itself. |
| 11. Çok eski zamanlardan bu yana, sonsuz insanları başka her sorudan daha
çok heyecana düşürmüştür. Hemen hemen başka hiçbir düşünce insan düşüncesini
böylesine verimli olarak uyarmamıştır. Gene de başka hiçbir kavram ondan daha çok durulaştırma gereksiniminde değildir. |
11. From time immemorial, the infinite has stirred men’s emotions more than any other question. Hardly any other idea has stimulated the
mind so fruitfully. Yet, no other concept needs clarification more than it does. |
— Sonsuzluk Kavramı Ve Heyecan
[‘Sonsuzluk kavramının yarattığı heyecanı sonsuzu bir nicelik olarak düşünen
bilinç çok geçmeden bir can sıkıntısı olarak yaşadığını görür.] |
| 12. Sonsuzun doğasını durulaştırma işine dönmeden önce, kısaca sonsuza
gerçekte hangi anlamın verildiğini belirtmeliyiz. İlkin fizikten ne öğrenebileceğimize bakalım. Kişinin doğal olaylar ve özdek
konusundaki ilk saf izlenimi kalıcılık, süreklilik izlenimidir. Bir parça metali ya da belli bir hacımdaki sıvıyı irdelediğimiz
zaman, sınırsızca bölünebilir oldukları, en küçük parçalarının bütün ile
aynı özellikleri sergilediği izlenimini ediniriz. Ama araştırma yöntemlerinin
özdek fiziğini yeterince inceltildiği her yerde, bilimciler çabalarının
eksikliğinden değil ama şeylerin doğasının kendisinden doğan bölünebilirlik
sınırları ile karşılaşmışlardır. Buna göre giderek modern
bilimin eğilimini sonsuz küçükten kurtulma olarak bile yorumlayabiliriz.
Eski natur non facit saltus ilkesi yerine, giderek karşıtını ileri
sürebiliriz: ‘‘doğa sıçramalar yapar.’’ |
12. Before turning to the task of clarifying the nature of the infinite,
we should first note briefly what meaning is actually given to the infinite.
First let us see what we can learn from physics. One’s first naive impression
of natural events and of matter is one of permanency, of continuity.
When we consider a piece of metal or a volume of liquid, we get the impression
that they are unlimitedly divisible, that their smallest parts exhibit the
same properties that the whole does. But wherever the methods of investigating
the physics of matter have been sufficiently refined, scientists have met
divisibility boundaries which do not result from the shortcomings of their
efforts but from the very nature of things. Consequently we could even
interpret the tendency of modern science as emancipation from the infinitely
small. Instead of the old principle natura non facit saltus, we
might even assert the opposite, viz., ‘‘nature makes jumps.’’ |
— Sonsuzluk Olgusal Olarak İrdeleniyor: Görgül Özdek Sonsuza Bölünebilir
Mi?
— Modern Bilim Sonsuzluk Kavramından Kurtulma Eğilimindedir |
13. Tüm özdeğin ‘‘atomlar’’ denilen ve bileşimleri ve bağıntıları tüm
mikroskopik nesneler türlülüğünü üreten çok küçük yapı taşlarından oluştuğu yaygın olarak bilinir. Gene de fizik özdeğin atomizminde durmadı.*
Geçtiğimiz yüzyılın sonunda ilk bakışta çok daha tuhaf görünen elektrik
atomizmi ortaya çıktı. O güne dek bir sıvı olarak düşünülmüş
ve sürekli etkin bir etmenin modeli olarak görülmüş olan elektriğin
o zaman pozitif ve negatif elektronlardan yapıldığı gösterildi. |
13. It is common knowledge that all matter is composed of tiny building
blocks called ‘‘atoms,’’ the combinations and connections of which produce
all the variety of macroscopic objects. Still physics did not stop at the
atomism of matter. At the end of the last century there appeared the atomism
of electricity which seems much more bizarre at first sight. Electricity,
which until then had been thought of as a fluid and was considered the model
of a continuously active agent, was then shown to be built up of positive
and negative electrons. |
—
Özdeğin Atomizmi
[‘Atom’ "asıl kavramında" modern fiziğin çekirdek
ve elektronlardan oluşan görgül tasarımı değildir. Gene de modern yazarlar
hiç de seyrek olmamak üzere ‘top’ ya da ‘güneş dizgesi’ biçiminde tasarımlanan
atomun bölünebilirliğinin gösterilmesiyle antik Atom kavramının çürütüldüğünü
ve böylece modern düşüncenin antik düşünceye karşı üstünlüğünün gösterildiğine
inanırlar. Gerçekte bu durum modern görgül ya da analitik düşüncenin henüz
çocuksu bir düşünce olduğunun ve analitik oldukça her zaman böyle kalacağının
tanıtıdır.] |
14. Özdek ve elektriğe ek olarak, fizikte kendisi için sakınım yasasının
geçerli olduğu bir başka kendilik, e.d. enerji vardır. Ama enerjinin bile
sonsuz bölünebilirliği koşulsuz olarak kabul etmediği doğrulanmıştır. Planck enerji nicelerini keşfetmiştir.* |
14. In addition to matter and electricity, there is one other entity in
physics for which the law of conservation holds, viz., energy. But it has
been established that even energy does not unconditionally admit of infinite
divisibility. Planck has discovered quanta of energy. |
*[Yine
vurgulanan şey özdeğin olduğu gibi enerjinin de sonsuza dek bölünemez olduğu,
belli bir quantum sınırında bölünebilmenin sonuna ulaşıp orada kaldığıdır.
Ama bu hiç kuşkusuz Kant’ın da usun bir çatışkısı diyecek olduğu şeydir.
Çünkü her quantum / nice, salt "belirli bir nicelik" olduğu için, bölünmeyi kabul eder. Analitik düşünce çatışkıyı görür.
Kant çatışkının çözülemez bir sorun yarattığını söyler. Analitik düşünce
yanlardan birini doğrular. Ve doyum içinde uslamlamasını sürdürür. Ama
eğer karşı savı da algılayacak olursa, Paradoks! diye bağırır. Paradoks
çatışkının analitik Anlak için çözümsüz biçimidir.] |
15. Bu nedenle, sonsuz ölçüde küçük olanı olgusallaştırmak için gerekli
olan bölünebilirlik türünü kabul eden türdeş
bir süreklilik [continuum] olgusallıkta hiçbir yerde bulunmaz. Bir süreklinin sonsuz bölünebilirliği yalnızca düşüncede varolan
bir işlemdir. Yalnızca bir düşüncedir ki gerçekte doğa üzerine gözlemlerimizin
ve fiziksel ve kimyasal deneylerimizin sonuçları tarafından çürütülür. |
15. Hence, a homogeneous continuum which admits of the sort of divisibility
needed to realize the infinitely small is nowhere to be found in reality.
The infinite divisibility of a continuum is an operation which exists only
in thought. It is merely an idea which is in fact impugned by the results
of our observations of nature and of our physical and chemical experiments. |
—
Türdeş Süreklilik Olgusallıkta Bulunmaz;
Sonsuza Bölünebilirlik Bir Yanılsamadır |
| 16. Sonsuzun doğada bulunup bulunmadığı sorusu ile karşılaştığımız ikinci yer bir bütün olarak evrenin irdelemesidir.
Burada sonsuz ölçüde büyük birşeyi kapsayıp kapsamadığını belirlemek için evrenin genişliğini irdelememiz gerekir.
Ama yine burada modern bilim, özellikle gökbilim, soruyu yeniden açmıştır
ve çözmeye çalışmaktadır — metafiziksel kurgunun özürlü yöntemi ile değil,
ama deney üzerine ve doğa yasalarının uygulaması üzerine dayalı nedenler
yoluyla.* Burada da sonsuzluğa yönelik ciddi karşıçıkışlar bulunmuştur. Euklides geometrisi zorunlu olarak uzayın sonsuz olduğu konutlamasına götürür.
Ama Euklides geometrisinin gerçekten de tutarlı bir kavramsal dizge olmasına
karşın, bundan Euklides geometrisinin olgusallıkta
edimsel olarak geçerli olduğu sonucu çıkmaz. Uzayın
Euklides geometrisine uygun olup olmadığı ancak gözlem ve deney yoluyla
belirlenebilir.** Uzayın sonsuzluğunu arı kurgu yoluyla tanıtlama
girişimi kaba yanılgılar kapsar. Belli bir uzay parçasının dışında her
zaman daha çok uzay olması olgusundan yalnızca uzayın sınırsız olduğu sonucu çıkar, sonsuz olduğu değil. Sınırlanmamışlık ve sonluluk
bağdaşabilirdirler. Eliptik denilen geometride, matematiksel araştırma
doğal bir sonlu evren modeli sunar.*** Bugün Euklides geometrisinin
terkedilmesi yalnızca matematiksel ya da felsefi bir kurgu değildir, ama
başlangıçta evrenin sonluluğu sorusu ile hiçbir ilgileri olmayan irdelemeler
tarafından ileri sürülmüştür. Einstein Euklides
geometrisinin terk edilmesi gerektiğini göstermiştir. Einstein kendi yerçekimi
kuramının temelinde, evrenbilimsel soruları ele alır ve sonlu
bir evrenin olanaklı olduğunu gösterir.**** Dahası, gökbilimin
tüm sonuçları evrenin eliptik olduğu konutlaması ile eksiksiz olarak bağdaşabilirdir. |
16. The second place where we encounter the question of whether the infinite
is found in nature is in the consideration of the universe as a whole. Here
we must consider the expanse of the universe to determine whether it embraces
anything infinitely large. But here again modern science, in particular
astronomy, has reopened the question and is endeavoring to solve it, not
by the defective means of metaphysical speculation, but by reasons which
are based on experiment and on the application of the laws of nature. Here,
too, serious objections against infinity have been found. Euclidean geometry necessarily leads to the postulate that space is infinite. Although
euclidean geometry is indeed a consistent conceptual system, it does not
thereby follow that euclidean geometry actually holds in reality. Whether
or not real space is euclidean can be determined only through observation
and experiment. The attempt to prove the infinity of space by pure speculation
contains gross errors. From the fact that outside a certain portion of space
there is always more space, it follows only that space is unbounded, not
that it is infinite. Unboundedness and finiteness are compatible. In so-called elliptical geometry, mathematical investigation furnishes the natural
model of a finite universe. Today the abandonment of euclidean geometry
is no longer merely a mathematical or philosophical speculation but is suggested
by considerations which originally had nothing to do with the question of
the finiteness of the universe. Einstein has shown that euclidean geometry
must be abandoned. On the basis of his gravitational theory, he deals with
cosmological questions and shows that a finite universe is possible. Moreover,
all the results of astronomy are perfectly compatible with the postulate
that the universe is elliptical. |
—
Euklides Geometrisi: Mantıksal Olarak Uzay Sonsuzdur
— Euklides Geometrisinin Gerçekliğini
Gözlem Ve Deney Doğrulamalıdır [Burada Hilbert bir kez daha tipik pozitivist
konumu doğrular: Kuram olgu tarafından doğrulanmalıdır. Ama olgunun kendisinin özsel olarak "kavramsal" olduğu gerçeği bizi kuramın ancak kuram tarafından, mantığın ancak mantık
tarafından sınanabileceği kavrayışına götürür. Hilbert pozitivizmin bu yalın
mantıksal gerçeği gözden kaçıran saflığının bilincinde değildir.]
— Euklides Geometrisini Terketmenin
Gerekçeleri
— Einstein Euklides Geometrisinin
Terkedilmesi Gerektiğini Göstermiştir |
*Hilbert
bilinen önyargı üzerine oynuyor. ‘Deneyler’ yoluyla, ‘gökbilimsel gözlem’
yoluyla ‘sonsuzluk’ sorununun çözülebileceğinden söz etmek hiç kuşkusuz
kötü metafizik ya da mantıksızlık denilen şey olmalıdır.
**Yine
istenen şey kavramsal bir dizgenin görgül veriler tarafından doğrulanmasıdır.
Felsefe, tersine, görgül olanın mantıksal olarak doğrulanması gerektiğini
ileri sürer. Aslında Ptolemi’den Galileo’ya, Kepler’den Newton’a dek soyut-kavramsal
geometri olgusal-nesnel uzay üzerinde uygulanmış, ve deneysel-görgül olanın
geometrik olan tarafından denetlendiği doğrulanmıştır (ya da yine de görgül
olana üstünlük vereceksek, görgül olan geometrik ya da a priori olanı
DIŞSAL OLARAK doğrulamıştır, bu olanaklıdır çünkü görgül olan en sonunda
kavramsal bir yapıdadır). (Kategorilerin görüngüyü belirlemesi bağlamında
Kant’a göndermede bulunmayı aklayabilecek tek şey felsefenin genel sorunlarının
özellikle onun tarafından popülerleştirilmiş olması ve Avrupa felsefeciliğinin
konuya yaklaşımlarında bir tür ölçün olarak özellikle onun formülasyonlarının
kullanılmasıdır.)
***Eliptik
geometri ya da Riemann geometrisi. Euklides geometrisine karşı ileri sürülen
almaşıklardan biri. Uzayı bir kürenin yüzeyi olarak varsayar ve böylece
Euklides geometrisinin bir küre yüzeyi üzerindeki dönüşümüdür. Hiç kuşkusuz
bu geometri kendi alanında hiçbir biçmde usdışı değildir ve Euklides’in
Öğeler’inin belitleri ile çelişmesi söz konusu değildir..
****Hilbert
nesnel olarak düşünmez, kavramın kendi mantığını izlemez, tersine olguları
önceden verdiği yargıya göre yorumlar: Görgüllük biricik gerçeklik ölçütü
olunca, hiç kuşkusuz ancak sonluluk doğrulanabilir, sonsuzluk değil (görgül
olan kavramı gereği sonludur). Ya da, salt görgül-duyusal olarak tanıtlanabilecek
olan doğrulanacaksa, Evren ancak sonlu olabilir. Ama bu saçmalığın sonsuzluğu
Evrenin sonsuzluğu ile yarışabilir. Çünkü hiçbir görgül kanıt, gözlem,
deneyim vb. evrenin ‘sonluluğunu’ dolaysızca göstermez, ve böylece sonluluğu
ileri sürmenin kendisi de salt kuramsal bir tutumdur. Görgücülük sözcüğün
en usdışı anlamında metafiziktir. |
17. Evrenin sonlu olduğunu iki açıdan, e.d.,
sonsuz ölçüde küçük ve sonsuz ölçüde büyük açısından saptadık. Ama sonsuz
gene de düşünmemizde haklı bir yer dolduruyor, ve vazgeçilemez bir kavram
rolünü oynuyor olabilir. Durumun matematikte ne olduğunu görelim. İlkin
insan anlığının en arı ve en yalın ürününü, e.d. sayı
kuramını irdeleyelim. Sayı kuramının öğesel formüllerinin varsıl
türlülüğünden tek bir formülü, örneğin şu formülü irdeleyelim:
12 + 22 + 32 + . . . + n2 = 1/6n(n + 1)(2n + 1)
|
17. We have established that the universe is finite in two respects, i.e.,
as regards the infinitely small and the infinitely large. But it may
still be the case that the infinite occupies a justified place in our thinking,
that it plays the role of an indispensable concept. Let us see what the
situation is in mathematics. Let us first interrogate that purest and
simplest offspring of the human mind, viz., number theory.
Consider one formula out of the rich variety of elementary formulas of number
theory, e.g., the formula
12 + 22 + 32 +. . . + n2 = 1/6n(n + 1)(2n + 1) |
— Evren
Sonsuz Küçükte Ve Sonsuz Büyükte Sonludur
— Sayı
Kuramı İrdeleniyor
[Hilbert
‘sonsuz ölçüde küçük’ ve ‘sonsuz ölçüde büyük’ birer sonludur der. Yazı
hiçbir irdelemeye değmez olan bu türden çelişkilerle dolup taşar.] |
18. n yerine ne olursa olsun herhangi bir tamsayı geçirebildiğimiz
için — örneğin n = 2 ya da n = 5 —, bu formül örtük olarak
sonsuz çoklukta önerme kapsar. Bu karakteristik bir formüle özseldir. Formülün
aritmetiksel bir problemin çözümünü temsil edebilmesini sağlar ve tanıtı
için özel bir düşünceyi zorunlu kılar.
Öte yandan, şu bireysel sayısal eşitlikler
12 + 22 = 1/6 · 2 · 3 · 5
12 + 22 + 32 + 42 + 52 = 1/6 · 5 · 6 · 11
yalnızca hesaplama
yoluyla doğrulanabilirler ve bu nedenle bireysel olarak hiçbir özel önemleri
yoktur. |
18. Since we may substitute any integer whatsoever for n, for example n = 2 or n = 5, this formula implicitly contains infinitely
many propositions. This characteristic is essential to a formula.
It enables the formula to represent the solution of an arithmetical problem
and necessitates a special idea for its proof.
On the other hand, the individual numerical equations
12 + 22 = 1/6 · 2 · 3 · 5
12 + 22 + 32 + 42 + 52 = 1/6 · 5 · 6 · 11
can
be verified simply by calculation and hence individually are of no especial
interest. |
19. Önemli ve verimli ideal öğeler yönteminde sonsuzun kavramının bütünüyle ayrı ve bütünüyle benzersiz bir
anlayışı ile karşılaşırız. İdeal öğeler yöntemi giderek öğesel düzlem
geometride bile kullanılır. Düzlemin noktaları
ve doğru çizgileri başlangıçta olgusal, edimsel olarak varolan nesnelerdir. Onlar için geçerli olan belitlerden biri bağıntı belitidir:
iki noktadan bir ve yalnızca bir doğru çizgi geçer. Bu belitten iki doğru çizginin en çoğundan tek bir noktada kesiştikleri beliti
çıkar. İki doğru çizgi her zaman bir noktada kesişirler gibi bir teorem
yoktur, çünkü iki doğru çizgi pekala koşut olabilir. Gene de ideal öğeleri,
e.d. sonsuz ölçüde uzun çizgileri ve sonsuzluktaki noktaları getirerek
iki doğru çizgi her zaman bir ve yalnızca bir noktada kesişirler teoreminin
evrensel olarak doğru çıkmasını sağlayabileceğimizi biliyoruz. Bu ideal
‘‘sonsuz’’ öğeler bağıntı yasaları dizgesini olanaklı olduğu ölçüde yalın
ve kolayca anlaşılır kılma üstünlüğünü taşırlar. Dahası, bir nokta ve
bir doğru çizgi arasındaki bakışım nedeniyle, geometri için o çok verimli
olan ikilik ilkesi doğar. |
19. We encounter a completely different and quite unique conception of the
notion of infinity in the important and fruitful method of ideal elements.
The method of ideal elements is used even in elementary plane geometry.
The points and straight lines of the plane originally are real, actually
existent objects. One of the axioms that hold for them is the axiom of connection:
one and only one straight line passes through two points. It follows from
this axiom that two straight lines intersect at most at one point. There
is no theorem that two straight lines always intersect at some point, however,
for the two straight lines might well be parallel. Still we know that by
introducing ideal elements, viz., infinitely long lines and points at infinity,
we can make the theorem that two straight lines always intersect at one
and only one point come out universally true. These ideal ‘‘infinite’’ elements
have the advantage of making the system of connection laws as simple and
perspicuous as possible. Moreover, because of the symmetry between a point
and a straight line, there results the very fruitful principle of duality
for geometry. |
— ‘İdeal Öğeler’; ‘Başlangıçta’ Reel Öğeler
[‘İdeal
öğeler’ anlatımı belitlerin, tanımların vb. ‘görgül’ kökenlerini vurgulamak
için getirilir.] |
20. İdeal öğelerin kullanımının bir başka örneği cebirin bir eşitliğin
köklerinin varoluşu ve sayısı konusundaki teoremleri yalınlaştırmaya hizmet
eden tanıdık karmaşık-imgesel büyüklükleridir. |
20. Another example of the use of ideal elements are the familiar complex-imaginary magnitudes of algebra which serve to simplify theorems about the existence
and number of the roots of an equation. |
21. Tıpkı sonsuz çoklukta doğru çizginin, e.d. birbirlerine koşut olan
çizgilerin geometride bir ideal noktayı tanımlamak için kullanılmaları
gibi, sonsuz çoklukta sayıların belli dizgeleri de bir ideal sayıyı tanımlamak için kullanılır. İdeal öğeler ilkesinin bu uygulaması tümü
içinde en dahice olanıdır. Eğer bu ilkeyi tüm cebir için dizgesel olarak
uygularsak, tam olarak 1, 2, 3, 4 . . . gibi tanıdık bütün sayılar
için geçerli olan o aynı yalın ve tanıdık bölme yasalarını elde ederiz.
Daha şimdiden yüksek aritmetiğin alanı içerisindeyiz. |
21. Just as infinitely many straight lines, viz., those parallel to each
other, are used to define an ideal point in geometry, so certain systems
of infinitely many numbers are used to define an ideal number. This
application of the principle of ideal elements is the most ingenious of
all. If we apply this principle systematically throughout an algebra, we
obtain exactly the same simple and familiar laws of division which hold
for the familiar whole numbers 1, 2, 3, 4, . . . . We are already
in the domain of higher arithmetic. |
22. Şimdi matematiğin en estetik ve en ince kuruluşlu yapısına, e.d. analize
geliyoruz. Daha şimdiden sonsuzluğun analizde öncü bir rol oynadığını
biliyorsunuz. Belli bir anlamda, matematiksel
analiz sonsuzun bir senfonisidir. |
22. We now come to the most aesthetic and delicately erected structure of
mathematics, viz., analysis. You already know that infinity plays the leading
role in analysis. In a certain sense, mathematical analysis is a symphony
of the infinite. |
23. Sonsuz küçüklük kalkülüsünde yapılan olağanüstü ilerleme başlıca sonsuz
çoklukta öğelerin matematiksel dizgeleri ile çalışmaktan doğar. Ama, sonsuzu
‘‘çok büyük’’ ile özdeşleştirmek çok usayatkın göründüğü için,
çok geçmeden bir ölçüde eski sofistlerin de bildikleri tutarsızlıklar,
sonsuz küçüklük kalkülüsünün o ünlü paradoksları doğar. Ama sonlu için
geçerli olan birçok teoremin (örneğin, parça bütünden küçüktür,
bir en küçük ve en büyüğün varoluşu, bir toplamın ya da çarpımın terimlerinin
düzeninin kendi içinde değiştirilebilirliği) dolaysızca ve sınırsızca
sonsuza genişletilemeyeceğinin anlaşılması temel ilerleme anlamına geliyordu.
Bu denemenin başında dediğim gibi, bu sorular özellikle Weierstrass’ın
keskin kavrayışı yoluyla tam olarak durulaştırılmışlardır. Bugün analiz
yalnızca kendi alanı içerisinde yanılmaz olmakla kalmaz, ama sonsuzu kullanmak
için de yararlı bir araç olmuştur. |
23. The tremendous progress made in the infinitesimal calculus results mainly
from operating with mathematical systems of infinitely many elements. But,
as it seemed very plausible to identify the infinite with the ‘‘very large,’’
there soon arose inconsistencies which were known in part to the ancient
sophists, viz., the so-called paradoxes of the infinitesimal calculus. But
the recognition that many theorems which hold for the finite (for example,
the part is smaller than the whole, the existence of a minimum and a maximum,
the interchangeability of the order of the terms of a sum or a product)
cannot be immediately and unrestrictedly extended to the infinite, marked
fundamental progress. I said at the beginning of this paper that these questions
have been completely clarified, notably through Weierstrass’s acuity. Today,
analysis is not only infallible within its domain but has become a practical
instrument for using the infinite. |
24. Ama analiz yalnız başına bize sonsuzun doğasına ilişkin en derin
içgörüyü vermez. Bu içgörüyü bizim için üreten şey genel bir felsefi düşünme
yoluna yaklaşan ve sonsuza ilişkin bütün sorular karmaşası üzerine yeni
bir ışık düşürmek için tasarlanan bir disiplindir. George
Cantor tarafından yaratılan bu disiplin küme kuramıdır. Bu
denemede, küme kuramının yalnızca Cantor’un öğretisinin asıl özeğini oluşturan
o benzersiz ve özgün parçası ile, e.d. sonluötesi sayılar kuramı
ile ilgileniyoruz. Bu kuram, sanırım, matematiksel dehanın en ince ürünüdür
ve insanın arı anlıksal etkinliğinin en yüksek başarımlarından biridir.
O zaman bu kuram nedir? |
24. But analysis alone does not provide us with the deepest insight into
the nature of the infinite. This insight is procured for us by a discipline
which comes closer to a general philosophical way of thinking and which
was designed to cast new light on the whole complex of questions about the
infinite. This discipline, created by George Cantor, is set theory. In this
paper, we are interested only in that unique and original part of set theory
which forms the central core of Cantor’s doctrine, viz., the theory of transfinite numbers. This theory is, I think, the finest product of mathematical genius
and one of the supreme achievements of purely intellectual human activity.
What, then, is this theory? |
— Cantor’un
Sonluötesi Sayılar Kuramı |
25. Sonsuz üzerine Cantor’un getirdiği yeni anlayışı kısaca nitelendirmek
isteyen biri diyebilir ki analizde sonsuz ölçüde büyük ve sonsuz ölçüde
küçük ile yalnızca sınırlayıcı kavramlar olarak, ‘oluş’ta olan,
olmakta olan birşey olarak ilgileniriz, e.d. gizil sonsuz ile ilgileniriz.
Ama bu gerçek sonsuz değildir. Gerçek sonsuz ile 1, 2, 3, 4, . . . gibi sayıların bütünlüğünün kendisini tamamlanmış bir birlik olarak gördüğümüz
zaman, ya da bir aralığın noktalarını şeylerin hep birden varolan bir
bütünlüğü olarak gördüğümüz zaman karşılaşırız. Bu sonsuzluk türü edimsel
sonsuzluk olarak bilinir. |
25. Someone who wished to characterize briefly the new conception of the
infinite which Cantor introduced might say that in analysis we deal with
the infinitely large and the infinitely small only as limiting concepts,
as something becoming, happening, i.e., with the potential infinite. But
this is not the true infinite. We meet the true infinite when we regard
the totality of numbers 1, 2, 3, 4, . . . itself as a completed unity,
or when we regard the points of an interval as a totality of things which
exists all at once. This kind of infinity is known as actual infinity. |
— Gizil Sonsuz: Oluş Sürecindeki Sonsuz
— Edimsel
Sonsuz: Bir Aralığın Noktaları
[Bunlar
ilk bakışta örneğin Hegel’in konuşma yolunda ‘kendinde’ sonsuz ve ‘kendi
için’ sonsuz kavramlarına karşılık düşüyor görünürler. Ama burada Hilbert’in
her ‘iki’ sonsuz biçimi de soyut nicelik alanında kalır.
Gizil sonsuz oluş sürecinde olan sonsuzdur, henüz sonsuz değil ama sonlu
bir nice, belirli bir sayıdır. Yalnızca ilerlemekte, ama hiçbir zaman
sonsuza erişememektedir. Böylece her sayı, örneğin 1, 2, . . . vb., ya
da giderek olumsuz sayılar bile birer gizil sonsuzdur, yeter ki ‘ilerliyor’
olsunlar. Doğal usumuz, ya da kurgul usumuz, böyle bir kurguyu kavramaya
yetenekli değildir. Öte yandan bunun diyalektik ile bir ilgisi de yoktur. Usun böyle birşeyi
doğrulamasının biricik yolu kendini yadsımak, usdışına geçmektir. Ve bilindiği
gibi usdışını doğrulamak insan usu için hiç de güç birşey değildir: Etki
nedeni öncelediği zaman, genişliksiz bir doğru olan çizgideki boyutsuz
noktalar sayıldığı zaman, ya da parça bütünden büyük olduğu zaman, uzaylar
bükülebildiği zaman, o zaman yer alan şey tam olarak usdışına geçiştir.
Bu
paragrafta Hilbert’in kendi ile çelişkileri bütünüyle açıkta yatar. Doğal
usumuzun yargılarına güvenmeliyiz.] |
26
a. Özellikle matematiğin temelleri üzerine çalışmaları ile ünlü
iki matematikçi olan Frege ve Dedekind birbirlerinden bağımsız olarak matematik için hem sezgiden hem de deneyimden bağımsız olan bir temel sağlamak için edimsel
sonsuzu kullandılar. Bu temel yalnızca arı mantık üzerine
kuruluydu ve yalnızca mantıksal olan tümdengelimlerden yararlanıyordu.
Dedekind giderek işi sonlu sayı kavramını sezgiden almayıp tersine bir sonsuz küme* kavramını kullanma
yoluyla mantıksal olarak türetmeye dek vardırdı. Ama edimsel sonsuz
kavramını dizgesel olarak geliştiren Cantor oldu. Sonsuzun daha önce sözü edilen iki örneğini irdeleyelim:
- 1, 2, 3, 4, . . . .
- 0 ve 1 aralığının noktaları, ya da, yine aynı şey, 0 ve 1 arasındaki
gerçek sayılar bütünlüğü.
|
26
a. Frege and Dedekind, the two mathematicians most celebrated for their
work in the foundations of mathematics, independently of each other used
the actual infinite to provide a foundation for arithmetic which was independent
of both intuition and experience. This foundation was based solely on pure
logic and made use only of deductions that were purely logical. Dedekind
even went so far as not to take the notion of finite number from intuition
but to derive it logically by employing the concept of an infinite set.
But it was Cantor who systematically developed the concept of the actual
infinite. Consider the two examples of the infinite already mentioned
- 1, 2, 3,
4, . . . .
- The points of the interval 0 to 1 or, what comes to the same thing, the
totality of real numbers between 0 and 1.
|
*[Burada
söyleme bütünüyle önemsiz birşey gibi ‘sonsuz küme’ tasarımı katılır.
‘Sonsuz küme’ gerçekte mantıksalın karşıtıdır: Burada top ‘sezgi’ye atılır,
çünkü sezgi imgelemin tüm olanağını kullanarak kendine öyle bir belirsizlik
yaratır ki, duruluğun yittiği bu ortamda saçmalık da anlamını yitirir.
Küme kavramı doğal ustaki ‘anlamından’ sıyrılır, ve sözde ‘sezgisel’ bir
yapıntı olur: Karşılaştırılabilir sonsuzlar gerçekte birer sonludurlar.
Lütfen
bir sonraki notu izleyin.] |
26
b. Bu örnekleri büyüklükleri bakış açısından irdelemek bütünüyle doğaldır.
Ama böyle irdeleme ortaya bugün her matematikçinin tanışık olduğu hayrete
düşürücü sonuçlar serer. Çünkü tüm kesirli sayılar kümesini, e.d. 1/2,
1/3, 1/4, . . ., 3/7, . . ., kesirlerini irdelediğimizde
görürüz ki — yalnızca büyüklüğünün bakış açısından — bu küme
tamsayılar kümesinden daha büyük değildir. Bu nedenle kesirli
sayılar olağan yolda sayılabilir, e.d. numaralanabilirdiler deriz. Aynı
şey sayıların tüm köklerinin kümesi için, aslında tüm cebirsel sayılar
kümesi için geçerlidir. İkinci örnek birinciye andırımlıdır. Oldukça şaşırtıcıdır
ki, bir karenin ya da küpün tüm noktalarının
kümesi 0 ve 1 aralığının noktalarının kümesinden daha büyük
değildir.* Tüm sürekli işlevler kümesi için de bu böyledir. Bu olguları ilk kez öğrenmeniz üzerine, büyüklük bakış açısından yalnızca tek
bir benzersiz sonsuz olduğunu düşünebilirsiniz. Hiç
de değil! (1) ve (2)’nci örneklerdeki kümeler, bizim deyimimiz ile,
‘‘eşdeğer’’ değildir. Tersine, küme (2)
numaralanamaz, çünkü küme (1)’den daha büyüktür. ** Cantor’un kuramında
yeni ve özgün olan ile bu noktada karşılaşırız. Bir aralığın noktaları olağan
yolda, e.d. 1, 2, 3 . . . diye sayılamaz. Ama, edimsel sonsuzu
kabul ettiğimize göre, burada durmamız gerekmez. 1, 2, 3 . . . diye
saydığımızda, böyle numaralanan nesneleri hep birden tikel bir düzende
varolan bir sonsuz küme olarak görebiliriz.
Eğer, Cantor’u izleyerek, bu tip düzene w dersek, o zaman sayma doğallıkla w + 1, w + 2, . . . ile w + w ya dek ya da w · 2 ye dek sürer, ve sonra yine
(w · 2) + 1, (w · 2) + 2, + (w · 2) + 3, . . . (w · 2) + w, ya da w · 3,
ve
dahası
w · 2, w · 3, w · 4, . . . w · w (ya da w2), w2 + 1 . . .,
öyle
ki sonunda şu tabloyu elde ederiz:
1,
2, 3, . . .
w, w + 1, w + 2, . . .
w · 2, (w · 2)
+ 1, (w · 2)
+ 2, .
. .
w · 3,
(w · 3)
+ 1, (w · 3)
+ 2, .
. .
.
.
.
w2, w2 + 1, .
. .
w2 + w, w2 + w · 2, + w2 + w · 3, . . .
w2 · 2, (w2 · 2) + 1, . . .
(w2 · 2) + w, (w2 · 2) + (w · 2), . .
.
w3 , .
. .
w4, . . .
.
.
.
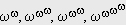
|
26
b. It is quite natural to treat these examples from the point of view
of their size. But such a treatment reveals amazing results with which every
mathematician today is familiar. For when we consider the set of all rational
numbers, i.e., the fractions 1/2, 1/3, 1/4, . . ., 3/7, . . .,
we notice that — from the sole standpoint of its size — this set is no larger
than the set of integers. Hence we say that the rational numbers can be
counted in the usual way; i.e., that they are enumerable. The same holds
for the set of all roots of numbers, indeed even for the set of all algebraic
numbers. The second example is analogous to the first. Surprisingly enough,
the set of all the points of a square or cube is no larger than the set
of points of the interval 0 to 1. Similarly for the set of all continuous
functions. On learning these facts for the first time, you might think that
from the point of view of size there is only one unique infinite. No, indeed!
The sets in examples (1) and (2) are not, as we say, ‘‘equivalent.’’ Rather,
the set (2) cannot be enumerated, for it is larger than the set (1). We
meet what is new and characteristic in Cantor’s theory at this point. The
points of an interval cannot be counted in the usual way, i.e., by counting
1, 2, 3, . . .. But, since we admit the actual infinite, we are not
obliged to stop here. When we have counted 1, 2, 3, . . ., we can
regard the objects thus enumerated as an infinite set existing all at once
in a particular order.
If, following Cantor, we call the type of this order w,
then counting continues naturally with w + 1, w + 2, . . . up to w + w or w · 2, and then again
(w · 2) + 1, (w · 2) + 2, + (w · 2) + 3, . . . (w · 2) + w, or w · 3,
and further
w · 2, w · 3, w · 4, . . . w · w (or w2), w2 + 1 . . .,
so that we finally
get this table:
1, 2, 3, . . .
w, w + 1, w + 2, . . .
w · 2, (w · 2)
+ 1, (w · 2)
+ 2, . .
.
w · 3,
(w · 3)
+ 1, (w · 3)
+ 2, . .
.
.
.
.
w2, w2 + 1, . .
.
w2 + w, w2 + w · 2, + w2 + w · 3, .
. .
w2 · 2, (w2 · 2) + 1, . . .
(w2 · 2) + w, (w2 · 2) + (w · 2), . . .
w3 , . .
w4, . . .
.
.
.
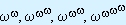 |
—
Tek Bir Benzersiz Sonsuz Yoktur
[*Şaşırtıcı
olan şey ‘‘bir karenin ya da kübün noktaları’’ anlatımıdır. Gerçekten
de 0 ve 1 aralığı ya da ne denli küçük olursa olsun herhangi bir ‘aralık’
salt kendi mantığı gereği, salt "niceliğin" doğası gereği, sonsuzun kendisidir: Ama böylelikle nicelik olmanın sınırına
gelir. Bir kübün, karenin ya da çizginin noktaları anlatımı ise "usdışıdır,"
daha doğrusu imgesel ya da ‘sezgisel’ denilen şeydir ki noktayı boyutsuzluktan
soyutlar. Bu bir kez kabul edildikten sonra sonsuz‘lar’dan
söz etmeye karşı çıkmak için hiçbir gerekçe kalmaz.
**Bir
sonsuz bir başka sonsuzdan daha büyüktür! Bu gerçekten de ‘özgün’ bir
noktadır, ve bu özgünlük yeni bir ussallığa mı yoksa bir usdışına, daha
doğrusu us-bölünmesine mi götürecektir, bunu göreceğiz.]
PASCAL,
‘‘Geometrik Anlık Üzerine’’ (De
l’esprit de géométrique, 1658)
 |
‘‘Ama
yalnızca zayıflığımız ile ilgili bu imgesel güçlüklerin karşısına
bırakalım şu doğal içgörüleri ve sağlam gerçeklikleri çıkarsınlar:
Eğer uzayın belli bir sonlu sayıda bölünmezden oluştuğu doğru
olsaydı, bundan her biri bir kare (eş deyişle, tüm kenarları eşit
ve benzer) ama biri ötekinin iki katı olan iki uzaydan birinin
bu bölünemezlerden ötekinin sayısının iki katını kapsayacağı sonucu
çıkardı. Bırakalım bu sonucu kafalarında sıkı sıkıya tutsunlar,
ve sonra noktalardan kareler yapma işine girişsinler, ta ki birinde
ötekinin noktalarının iki katı nokta olan iki kare buluncaya dek;
ve o zaman dünyadaki tüm geometricilerin onlara boyun eğmesini
sağlayacağım. Ama eğer bu doğallıkla olanaksızsa, daha açık olarak,
eğer noktalardan biri ötekinin noktalarının iki katını kapsayacak
kareler yapmada üstesinden gelinemez bir olanaksızlık varsa —
ki eğer harcanacak zamana değer olsaydı tam burada tanıtlardım
—, bırakalım gerekli vargıyı çıkarsınlar.’’
|
|
27. Bunlar Cantor’un ilk sonluötesi sayıları, ya da onun deyimiyle, ikinci sayı sınıfının
sayılarıdır. Onlara yalnızca saymayı olağan olarak numaralanabilir olan
sonsuzun ötesine genişleterek, e.d. olağan sonlu
saymanın doğal ve benzersiz olarak belirlenmiş tutarlı bir sürdürülmesi yoluyla varırız. Şimdiye dek bir kümenin yalnızca birinci,
ikinci, üçüncü, . . . üyesini saymamız gibi, şimdi de w inci, ( w + 1 )inci, . . . 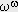 'inci üyeyi sayarız.* |
27. These are Cantor’s first transfinite numbers or, as he called them,
the numbers of the second number class. We arrive at them simply by extending
counting beyond the ordinarily enumerably infinite, i.e., by a natural and
uniquely determined consistent continuation of ordinary finite counting.
As until now we counted only the first, second, third, . . . member
of a set, we now count also the wth, (w + 1)st, . . ., 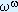 th member. th member. |
*Tüm
yapaylığının dışında, bu işlem ‘‘herhangi bir sayı’’ ile yapılan bir işlemdir,
ve ‘‘sonsuzun ötesine sayma’’ anlatımı ‘‘sonsuzu’’ edimsel olarak ‘‘sonluötesi,’’
ya da ‘‘herhangi bir’’ sayı yapmak demektir. |
28. Bu gelişmeler verildiğinde, kişi doğallıkla sonluötesi sayıları kullanarak
olağan yolda sayılamayacak o kümeleri gerçekten sayıp sayamayacağını merak
eder. |
28. Given these developments one naturally wonders whether or not, by using
these transfinite numbers, one can really count those sets which cannot
be counted in the ordinary way. |
29. Bu kavramlar temelinde, Cantor sonluötesi sayılar kavramını bütünüyle
başarılı olarak geliştirdi ve onlar için tam bir kalkülüs icadetti. Böylece,
Frege, Dedekind ve Cantor’un Herküllere yaraşır işbirlikleri ile, ‘sonsuz’
kral yapıldı ve büyük bir utkunun saltanatını yaşadı. Gözüpek bir uçuşla,
‘sonsuz’ baş döndürücü bir başarı doruğuna ulaşmıştı. |
29. On the basis of these concepts, Cantor developed the theory of transfinite
numbers quite successfully and invented a full calculus for them. Thus,
thanks to the Herculean collaboration of Frege, Dedekind, and Cantor, the
infinite was made king and enjoyed a reign of great triumph. In daring
flight, the infinite had reached a dizzy pinnacle of success. |
30. Ama tepkiler eksik olmadı. Gerçekte çok dramatik bir biçim aldı.
Sonsuz küçüklük kalkülüsünün gelişimine karşı tepkinin yerleşmesine tam
olarak andırımlı bir yolda yerleşti. Yeni ve önemli sonuçlar keşfetmenin
sevinci içinde, matematikçiler tümdengelimli yöntemlerinin geçerliğine
çok az dikkat ettiler. Çünkü, yalnızca geleneksel olmuş olan tanımları
ve tümdengelimli yöntemleri kullanmanın bir sonucu olarak, yavaş yavaş
çelişkiler ortaya çıkmaya başladı. Bu çelişkiler, küme kuramının ünlü
paradoksları, ilkin dağınık olmalarına karşın, giderek artan bir biçimde
iveğen ve daha ciddi olmaya başladılar. Özel olarak, Zermelo ve Russell tarafından ortaya çıkarılan bir çelişki matematik dünyası
içerisinde duyulduğu zaman açıkça yıkıcı bir etki yarattı. Bu paradokslar
ile karşı karşıya kalan Dedekind ve Frege bakış açılarını
tam olarak terkedip geri çekildiler. Dedekind Was sind und was
sollen die Zahlen [Sayılar Nedir ve Ne Olmaları Gerekir?] başlığı
altında çığır açıcı incelemesinin yeni bir düzenlemesinin yayımlanmasına
izin vermeden önce uzun bir süre kararsız kaldı. Bir sonsözde Frege de Grundgesetze der Mathematik [Matematiğin Temel Yasaları]
başlıklı kitabının yönünün yanlış olduğunu kabul etmek zorunda
kaldı. Cantor’un öğretisi de her yandan saldırıya uğradı. Bu tepki
öylesine yeğindi ki giderek matematiğin en sıradan ve verimli kavramları
ve en yalın ve en önemli tümdengelimli yöntemleri gözdağı altına düştüler
ve kullanımları geçersiz sayılma noktasına geldi. Eski düzenin hiç kuşkusuz
kendi savunucuları vardı. Bununla birlikte, savunma taktikleri çok fazla
yüreksizdi ve hiçbir zaman dirimsel noktalarda birleşik bir cephe oluşturmadı.
Paradokslar için birçok değişik çareler teklif edildi, ve onları durulaştırmak
için önerilen yöntemlere gereğinden öte türlülük görünüşü verildi. |
30. But reaction was not lacking. It took in fact a very dramatic form.
It set in perfectly analogously to the way reaction had set in against the
development of the infinitesimal calculus. In the joy of discovering
new and important results, mathematicians paid too little attention to the
validity of their deductive methods. For, simply as a result of employing
definitions and deductive methods which had become customary, contradictions
began gradually to appear. These contradictions, the so-called paradoxes
of set theory, though at first scattered, became progressively more acute
and more serious. In particular, a contradiction discovered by Zermelo
and Russell had a downright catastrophic effect when it became known throughout
the world of mathematics. Confronted by these paradoxes, Dedekind and
Frege completely abandoned their point of view and retreated. Dedekind
hesitated a long time before permitting a new edition of his epoch-making
treatise Was sind und was sollen die Zahlen to be published. In
an epilogue, Frege too had to acknowledge that the direction of his book Grundgesetze der Mathematik was wrong. Cantor’s doctrine, too,
was attacked on all sides. So violent was this reaction that even the
most ordinary and fruitful concepts and the simplest and most important
deductive methods of mathematics were threatened and their employment was
on the verge of being declared illicit. The old order had its defenders,
of course. Their defensive tactics, however, were too fainthearted and
they never formed a united front at the vital spots. Too many different
remedies for the paradoxes were offered, and the methods proposed to clarify
them were too variegated.
|
—
Frege Matematiğin ‘Temel Yasaları’nı Keşfeder; Sonra Bu Temelleri Geri
Çeker; Matematik Ayaktadır |
31. Kabul edilecektir ki, paradokslara çattığımız yerde işlerin durumu
dayanılmaz olur. Yalnızca herkesin matematikte, gerçeklik ve pekinliğin
benzersiz örneğinde öğrendiği, öğrettiği ve kullandığı tanımların ve tümdengelimci
yöntemlerin saçmalıklara götürdüğünü düşünün! Eğer matematiksel düşünme
kusurlu ise, gerçeklik ve pekinliği nerede bulacağız?* |
31. Admittedly, the present state of affairs where we run up against the
paradoxes is intolerable. Just think, the definitions and deductive methods
which everyone learns, teaches, and uses in mathematics, the paragon of
truth and certitude, lead to absurdities! If mathematical thinking is defective,
where are we to find truth and certitude? |
*Matematiksel
uslamlama örneği hiç kuşkusuz usun en yalın işlemlerini sergiler ve nesnesinin
‘‘duyulura yakın’’ olması ölçüsünde uslamlamaya sıradan bilinci doyuran
bir tür ‘‘duyusal’’ ek destek veriyor görünür. Bu yanıyla matematiksel
uslamlama pekinlik ve ussallığın ‘‘benzersiz örneği’’ olarak gösterilir.
Ama ‘‘kavram’’ın kendi eytişimi pekinliğin ve gerçekliğin ‘‘örneği’’ değil,
tersine kendisidir, ve onun için matematikten andırım saltık olarak gereksizdir.
Kendisi insan düşüncesinin bir ürünü ya da açınımı olduğu içindir ki matematiğe
içine düştüğü sorunlarda, çatışkı ya da paradoks ile karşılaştığında çözümü
yine kurgul düşünce sunar, onu kavramaksızın da nasıl ilerleyebildiğini,
soyutlamacı anlağın bu bilinçsiz başarısının gizinin nerede yattığını
ancak felsefeye özgü özel düşünce yolu açıklayabilir.
Sonsuz
küçüklükler sorununda Newton’un eytişimi nasıl kullandığını, sonsuz küçüklüğü
‘‘yiten büyüklük’’ olarak nasıl kavranabilir kıldığını görmek analitik
anlağın tek-yanlı yetisinin ötesine geçmeyi gerektirir. Bu konuda Newton’un
‘‘doğan’’ ve ‘‘yiten’’ [‘‘nascent’’ ve ‘‘evanescent’’] nicelikleri nasıl
irdelediği, ‘‘yiten niceliklerin oranları’’ konusuna nasıl yaklaştığı
incelenebilir. Bu konu için kz. ‘‘Principia’’da ‘‘Yardımcı Önerme 11’e
Not.’’ Newton hiç kuşkusuz bu eytişimsel uslamlamanın tam imlemlerinin
bilincinde değildir, aslında eytişim onun bütün bir görgücü düşünce yoluna
dışsaldır. Bu düzeye dek, Newton orada kendi öncellerinin analizlerini
yineler. |
32. Bununla birlikte, paradokslardan bilimimize ihanet etmeden kaçmanın
tam olarak doyurucu bir yolu vardır. Bize bu yolu bulmada yardım edecek
ve hangi yolu alacağımız gösterecek olan istekler ve tutumlar şunlardır:
- Nerede bir kurtarma umudu varsa, verimli tanımları ve tümdengelimci
yöntemleri dikkatle araştıracağız. Onları besleyecek, onları güçlendireceğiz.
Hiç kimse bizi Cantor’un bizim için yaratmış
olduğu cenneten kovamaz.
- Matematiğin her yanında tümdengelimlerimiz için hiç kimsenin kuşku
duymadığı ve orada çelişkilerin ve paradoksların yalnızca bizim dikkatsizliğimizden
doğduğu olağan öğesel sayı kuramında varolan aynı pekinliği sağlamalıyız.
33. Açıktır ki bu hedeflere ancak sonsuzun doğasını tam
olarak durulaştırmamızdan sonra ulaşılabilir.
|
32. There is, however, a completely satisfactory way of avoiding the paradoxes
without betraying our science. The desires and attitudes which will help
us find this way and show us what direction to take are these:
- Wherever there is any hope of salvage, we will carefully investigate
fruitful definitions and deductive methods. We will nurse them, strengthen
them, and make them useful. No one shall drive us out of the paradise which
Cantor has created for us.
- We must establish throughout mathematics the same certitude for our deductions
as exists in ordinary elementary number theory, which no one doubts and
where contradictions and paradoxes arise only through our own carelessness.
33. Obviously these goals can be attained only after we have fully
elucidated the nature of the infinite. |
34. Hangi deneyimlere, gözlemlere ya da bilgilere başvurulursa vurulsun, sonsuzun olgusallıkta
hiçbir yerde bulunmayacağını daha şimdiden gördük. Şeylere ilişkin
düşünce şeylerden böylesine ayrı olabilir mi? Düşünme süreçleri şeylerin
edimsel süreçlerine böylesine benzemez olabilir mi? Kısaca, düşünce
olgusallıktan böylesine uzak olabilir mi? Tersine, sonsuz ile belli
bir olgusal anlamda karşılaştığımızı düşündüğümüzde, böyle düşünmeye yalnızca
sık sık aşırı ölçüde büyük ve aşırı ölçüde küçük boyutlarla karşılaşmamız
olgusu tarafından ayartılmış olduğumuz açık değil midir?* |
34. We have already seen that the infinite is nowhere to be found in reality,
no matter what experiences, observations, and knowledge are appealed to.
Can thought about things be so much different from things? Can thinking
processes be so unlike the actual processes of things? In short, can
thought be so far removed from reality? Rather is it not clear that,
when we think that we have encountered the infinite in some real sense,
we have merely been seduced into thinking so by the fact that we often encounter
extremely large and extremely small dimensions in reality? |
—
Düşünce Ve Olgusallık İlişkisi Sorgulanıyor
*"Şey" bir yanda ve "Düşünce" öte yanda. Gerçekten
de bu iki kavramın "aynı" olmaları özlemi yerine getirilecek olsaydı
yalnızca analitik bir aynılık ile kalmazlar, ama analitik birer "yokluk" olurlardı.
Düşünce ve Şey karşıtlığının anlattığı şey burada Kavram ve Nesne,
İdeallik ve Olgusallık gibi başka karşıtlıkların anlattıkları ile aynıdır.
Ama her kavram bir başkasına indirgenemeyecek birşeydir, ve kendi
özgünlüğü ya da belirliliği vardır. Eğer ‘ayrılık’ ya da ‘özdeşsizlik’
sorunsa, onu yalnızca Düşünce ve Şey olarak değil, rasgele alınan her
kavram çifti arasında da görebiliriz, ve niçin bunlar birbirlerinden böylesine
uzak diye sorabiliriz. Sorun her kavramı kendi "bağımsızlığı" içinde
ya da "kendi için" de tanımak ve aynı zamanda bu bağımsızlığının
soyut bir ilişkisizlik olarak değil ama dizgesel bir ilişkiler bütününün
içerisinde değer taşıdığını görmektir. |
35. Özdeksel
mantıksal tümdengelim her nasılsa bizi aldatır ya da onu olgusal şeylere
ya da olaylara uyguladığımız zaman bizi yüzüstü mü bırakır? 1 Hayır. Özdeksel
mantıksal tümdengelim vazgeçilmezdir. Bizi ancak keyfi soyut tanımlar,
özellikle sonsuz çoklukta nesneler içeren tanımlar oluşturduğumuz
zaman aldatır. Böyle durumlarda özdeksel mantıksal tümdengelimi geçersiz
olarak kullanmışızdır, e.d. geçerli kullanımı için zorunlu önkoşullara
yeterince dikkat etmemişizdir. Dikkate alınması gereken böyle önkoşulların
olduğunu kabul edince, kendimizi felsefeciler ile, özellikle Kant ile anlaşma içinde buluruz. Kant matematiğin mantıktan
bağımsız olarak verili olan bir konuyu ele aldığını öğretti — ve bu
öğretisinin tümleyici bir parçasıdır. Matematik öyleyse yalnızca mantık
üzerine kurulamaz. Buna göre, Frege’nin ve Dedekind’in onu böyle temellendirme
girişimleri başarısızlığa mahkumdu.
1[Bu
denemenin tümünde Almanca ‘inhaltlich’ sözcüğü [sft] ‘özdeksel’ ya
da [blt] ‘özdeksel olarak’ sözcükleri ile çevrilmiştir; sözcükler
bu amaç için ayrılmıştır ve özdek ya da içerik ve mantıksal biçim
arasındaki geleneksel ayrımın anlamında özdeğe göndermede bulunmak
için kullanılırlar. — İng.’ye çevirenlerin notu.]
|
35. Does material logical deduction somehow deceive us or leave us in
the lurch when we apply it to real things or events?1 No! Material
logical deduction is indispensable. It deceives us only when we form arbitrary
abstract definitions, especially those which involve infinitely many objects.
In such cases we have illegitimately used material logical deduction;
i.e., we have not paid sufficient attention to the preconditions necessary
for its valid use. In recognizing that there are such preconditions that
must be taken into account, we find ourselves in agreement with the philosophers,
notably with Kant. Kant taught — and it is an integral part of his doctrine
— that mathematics treats a subject matter which is given independently
of logic. Mathematics, therefore, can never be grounded solely on logic.
Consequently, Frege’s and Dedekind’s attempts to so ground it were doomed
to failure.
1[Throughout
this paper the German word ‘inhaltlich’ has been translated by the words
‘material’ or ‘materially’ which are reserved for that purpose and which
are used to refer to matter in the sense of the traditional distinction
between matter or content and logical form. — Tr.] |
—
Öznel Tümdengelim Ve Nesnel İçerik (= Olgusal/Fiziksel Dünya)
— Kant:
Matematik Ve Mantık [Matematik mantık üzerine kurulamaz: Bu sava karşı
yanıtımız şu olmalıdır: Mantık üzerine kurulamayan hiçbirşey yoktur, mantıksız
olanın dışında.]
(İngilizce’de
‘inhaltlich’ için ‘contently’ türetmesi semantik bir sorun yaratmamasına
karşın dil beğenisine aykırıdır. Bu Türkçe için böyle değildir, ve ‘içeriksel’
sözcüğü Almanca sözcüğü tam olarak karşılar. Ama çeviri İngilizce’den
yapıldığı için ‘özdeksel’ sözcüğü korundu. Bunun dışında, gerçekte bu
bağlamda Hilbert’in içerik ile anlatmak istediği şey ‘duyulur’ olan olduğu
ölçüde, ‘özdeksel’ sözcüğü bu bütün usdışı söyleme daha uygundur.)] |
36. Mantıksal tümdengelimi kullanmak ve mantıksal işlemleri yürütmek için
daha öte bir önkoşul olarak tasarımda birşey verili olmalıdır,
e.d. tüm düşünmeye önsel olarak doğrudan deneyimlendikleri gibi sezilen
belli mantık-dışı somut nesneler. Mantıksal tümdengelimin pekin
olması için, bu nesnelerin her yanını görebilmeliyiz, ve özellikleri, ayrımları, ardışıklıkları ve bitişiklikleri,
nesnelerin kendileri ile birlikte, başka birşeye indirgenemeyen ve hiçbir
indirgeme gerektirmeyen birşey olarak verilmelidir. Bu benim yalnızca
matematik için değil, ama tüm bilimsel düşünme, anlama ve iletişim için
zorunlu gördüğüm temel felsefedir. Matematiğin konusu, bu kuram
ile uyum içinde, yapıları dolaysızca açık ve tanınabilir olan somut simgelerin kendileridir. |
36. As a further precondition for using logical deduction and carrying out
logical operations, something must be given in conception, viz., certain
extralogical concrete objects which are intuited as directly experienced
prior to all thinking. For logical deduction to be certain, we must be able
to see every aspect of these objects, and their properties, differences,
sequences, and contiguities must be given, together with the objects themselves,
as something which cannot be reduced to something else and which requires
no reduction. This is the basic philosophy which I find necessary not just
for mathematics, but for all scientific thinking, understanding, and communicating.
The subject matter of mathematics is, in accordance with this theory, the
concrete symbols themselves whose structure is immediately clear and recognizable. |
—
Matematik Görsel Bir Bilimdir
— Matematiğin Konusu Simgelerdir
[ 1)
Mantıksal tümdengelim ya da çıkarsama için tasarımsal (‘mantık-dışı’)
birşey verili olmamalıdır. Tasarımsal olan
mantıksal olan değil ama dahaçok çağrışımsal olandır (David Hume’un hizmetlerini
anımsayalım). Mantıksal ilişki zorunlu ilişkidir, başka türlü olamaz.
Tasarımlar arasındaki ilişki salt belleme ya da çağrışım ilişkisidir
ki olumsaldır, ve salt bu nedenle hiçbir bilimsel gerişimin temeli olamaz.
2)
‘Düşünmeye önsel olan nesneler’: Ama ‘nesne’nin kendisi ‘bir
evrensel = bir düşünce’dir. (Hilbert sağın bir mantık izlediği sanısı
içindedir.)
3)
‘Nesnelerin her yanını görebilmeliyiz’: Ek olarak dokunmak, tatmak, koklamak
da gerekmez mi?
4)
‘Matematiğin konusu ... simgelerin kendileridir.’ Eş deyişle, sayı, aritmetiksel
işlemler, sınır, türev, tümlev, ya da nokta, çizgi, yüzey, açı, koşutluk
vb. tümü de simgelerdir.
David
Hilbert’in MATEMATİK KAVRAMInın kendisinden yoksun olduğunu söylemek zorundayız.] |
37. Olağan sonlu sayılar kuramının doğasını ve yöntemlerini irdeleyin.
Hiç kuşkusuz sezgisel özdeksel irdelemeler yoluyla sayısal yapılardan
kurulabilir. Ama matematik hiç kuşkusuz yalnızca sayısal eşitliklerden
oluşmaz ve hiç kuşkusuz yalnızca onlara indirgenemez. Gene de matematiğin
tamsayılara uygulandığında her zaman doğru sayısal eşitlikler veren bir
aygıt olduğu ileri sürülebilir. Ama bu durumda henüz bu aygıtın gerçekte
her zaman doğru eşitlikler verdiğinden emin olmak için yapısını baştan
sona araştırmamız gerekir. Böyle bir araştırmayı yürütmek için, elimizde
yalnızca sayı kuramının kurulmasında sayısal eşitlikleri türetmek için
kullanılan o aynı somut özdeksel sonlu yöntemler vardır. Bu bilimsel
gerek gerçekte karşılanabilir, e.d., salt sezgisel ve sonlu bir yolda
— sayı kuramının gerçekliklerini elde ediş yolumuz — matematiksel aygıtın
geçerliğinin güvencesini veren içgörüleri elde etmek olanaklıdır. |
37. Consider the nature and methods of ordinary finitary number theory.
It can certainly be constructed from numerical structures through intuitive
material considerations. But mathematics surely does not consist solely
of numerical equations and surely cannot be reduced to them alone. Still
one could argue that mathematics is an apparatus which, when applied to
integers, always yields correct numerical equations. But in that event we
still need to investigate the structure of this apparatus thoroughly enough
to make sure that it in fact always yields correct equations. To carry out
such an investigation, we have available only the same concrete material
finitary methods as were used to derive numerical equations in the construction
of number theory. This scientific requirement can in fact be met, i.e.,
it is possible to obtain in a purely intuitive and finitary way-the way
we attain the truths of number theory-the insights which guarantee the validity
of the mathematical apparatus. |
| 38. Sayı kuramını daha yakından irdeleyelim. Sayı kuramında
1, 11, 111, 1111
gibi sayısal simgeler vardır ki burada her bir sayısal simge yalnızca 1'leri kapsaması olgusu yoluyla sezgisel olarak tanınabilir. Kendileri konumuz olan bu sayısal simgelerin kendilerinde hiçbir imlemleri yoktur. Ama bu simgelere ek olarak, giderek öğesel sayı kuramında bile, anlamları olan ve iletişimi kolaylaştırmaya hizmet eden başka simgeler isteriz; örneğin 2 simgesi 11 sayısal simgesi için bir kısaltma olarak, ve sayısal 3 simgesi sayısal 111 simgesi için bir kısaltma olarak kullanılır. Dahası, bildirimleri iletmek için +, = ve > gibi simgeleri kullanırız. 2 + 3 = 3 + 2 anlatımı 2 + 3'ün ve 3 + 2'nin, kısaltmalar dikkate alındığında, aynı sayısal simge, e.d. sayısal 11111 simgesi olduğu olgusunu iletmek için amaçlanır. Benzer olarak, 3 > 2 anlatımı 3 simgesinin, e.d. 111 simgesinin 2 simgesinden, e.d. 11'den daha uzun olduğu, ya da, başka bir deyişle, ikinci simgenin sözcüğün asıl anlamında birincinin bir parçası olduğu olgusunu iletmeye hizmet eder. |
38. Let us
consider number theory more closely. In number theory we have the numerical
symbols
1,
11, 111, 1111
where each numerical
symbol is intuitively recognizable by the fact it contains only 1’s. These
numerical symbols which are themselves our subject matter have no significance
in themselves. But we require in addition to these symbols, even in elementary
number theory, other symbols which have meaning and which serve to facilitate
communication, for example the symbol 2 is used as an abbreviation for
the numerical symbol 11, and the numerical symbol 3 as an abbreviation
for the numerical symbol 111. Moreover, we use symbols like +,
=, and > to communicate statements. 2 + 3 = 3 + 2 is intended to communicate
the fact that 2 + 3 and 3 + 2, when abbreviations are taken into account,
are the self same numerical symbol, viz., the numerical symbol 111111. Similarly 3 > 2 serves to communicate the fact that the
symbol 3, i.e., 111 , is longer than the symbol 2, i.e., 11; or, in other words, that the latter symbol is a proper part of
the former. |
—
Sayı Kuramının ‘Yakından’ İrdelenişi: Simgelerin Simgeleri, Vb
[Hilbert görünürde Klasik ve İslamik matematikçilerin simgeler kullanmadıkları
olgusundan da habersizdir. Burada simgelerin değil ama simgeleri oldukları
Kavramların tüm içerik ve tüm biçim olduğunu bir kez daha belirtmek gereksizdir.
Matematiği
Simgeciliğe indirgemesi Hilbert’in bir tutarsızlığı değil, tersine tutarlı
olmasının kaçınılmaz sonucudur. Duyusalcı bakış açısından düşünen birinin
sayı ussal bir dizgeye ait bir kavramdır demesini beklemeliyiz.] |
| 39. Ayrıca iletişim için a, b, c harflerini de kullanırız. Böylece b > a anlatımı sayısal b simgesinin sayısal a simgesinden daha uzun olduğu olgusunu
iletir. Bu bakış açısından a + b = b + a anlatımı
yalnızca sayısal a + b simgesinin b + a ile
aynı olduğu olgusunu iletir. Bu iletişimin içeriği özdeksel tümdengelim
yoluyla da tanıtlanabilir. Aslında, bu tür sezgisel özdeksel irdeleme bizi
çok uzağa götürebilir. |
39. We also use the letters a, b, c for communication. Thus b > a communicates the fact that the numerical symbol b is
longer than the numerical symbol a . From this point of view, a + b = b + a communicates only the fact that the numerical
symbol a + b is the same as b + a . The content
of this communication can also be proved through material deduction. Indeed,
this kind of intuitive material treatment can take us quite far. |
40. Ama
size bu sezgisel yöntemin nerede aşıldığı konusunda bir örnek
vereyim. Bilinen en büyük asal sayı şudur (39 basamak):
p = 170 141
183 460 469 231 731 687 303 715 884 105 727
Euklides’e bağlı
iyi bilinen bir yöntem yoluyla p + 1 ve p! + 1 arasında
en azından yeni bir asal sayı vardır bildiriminin bir tanıtını, bütünüyle
sonlu çerçevemiz içerisinde kalan bir tanıtını verebiliriz. Bildirimin
kendisi sonlu yaklaşımımıza eksiksiz olarak uygun düşer, çünkü ‘‘vardır’’
anlatımı yalnızca şu anlatımı kısaltmaya yarar: açıktır ki p + 1 ya da p + 2 ya da p + 3 . . . ya da p!
+ 1 bir asal sayıdır. Dahası, bir asal sayı vardır ki
1._> p dir, ve aynı zamanda
2._ =< p! + 1 dir
demek açıkça aynı şeye vardığı için, Euklides kuramının anlattığının
yalnızca bir parçasını anlatan bir teoremi, e.d. bir ‘asal sayı > p’ vardır teoremini formüle etmeye götürülürüz. Gerçi
bu teorem içerik terimlerinde çok zayıf olsa da — Euklides teoreminin
ileri sürdüğünün yalnızca bir bölümünü ileri sürer —, ve gerçi Euklides
teoreminden buna geçiş bütünüyle zararsız görünse de, gene de bölümsel
bildirim bağlamın dışına alınıp bağımsız bir bildirim olarak görüldüğü
zaman bu geçiş sonluötesine bir sıçrayışı gerektirir.
|
40. But let me give you an example where this intuitive method is outstripped.
The largest known prime number is (39 digits)
p = 170 141 183 460 469 231 731 687 303 715 884 105 727
By a
well-known method due to Euclid we can give a proof, one which remains
entirely within our finitary framework, of the statement that between p + 1 and p! + 1 there exists at least one new prime number.
The statement itself conforms perfectly to our finitary approach, for
the expression ‘there exists’ serves only to abbreviate the expression:
it is certain that p + 1 or p + 2 or p + 3 . .
. or p! + 1 is a prime number. Furthermore, since it obviously
comes down to the same thing to say: there exists a prime number which
1._> p, and at the same time is
2._ =< p! + 1,
we are led to formulate a theorem which expresses only a part of what
the euclidean theorem expresses; viz., the theorem that there exists a
prime number > p. Although this theorem is a much weaker
statement in terms of content — it asserts only part of what the euclidean
theorem asserts — and although the passage from the euclidean theorem
to this one seems quite harmless, that passage nonetheless involves a
leap into the transfinite when the partial statement is taken out of context
and regarded as an independent statement. |
| 41. Bu
nasıl olabilir? Çünkü varoluşsal bir bildirimimiz vardır: ‘‘vardır’’!
Doğru, Euklides teoreminde benzer bir anlatımımız vardı, ama orada
‘‘vardır’’ anlatımı, daha önce belirttiğim gibi, p + 1 ya
da p + 2 ya da p + 3 ya da p! + 1 bir asal
sayıdır anlatımı için bir kısaltmaydı — tıpkı ‘‘ya bu tebeşir parçası
ya da bu parça ya da bu parça . . . ya da bu parça kırmızıdır’’
demek yerine, kısaca ‘‘bu parçalar arasında bir kırmızı tebeşir
parçası vardır’’ dediğimiz zaman olduğu gibi. Bir sonlu bütünlükte
belli bir özelliği olan bir nesne ‘‘vardır’’ gibi bir bildirim sonlu
yaklaşımımıza eksiksiz olarak uygun düşer. Ama ‘ p + 1 ya
da p + 2 ya da p + 3 . . . ya da (sonsuza dek) . . . belli bir özellik taşır’ gibi bir bildirimin kendisi
sonsuz bir mantıksal üründür. Sonsuza doğru böyle bir genişleme,
elimizde daha öte açıklama ve önlemler olmadıkça, kalkülüste sonludan
sonsuz ürünlere genişlemenin olduğundan daha kabul edilebilir değildir.
Böyle genişlemeler, buna göre, genellikle anlamsızlığa düşerler.
|
41. How
can this be? Because we have an existential statement, ‘‘there exists’’! True, we
had a similar expression in the euclidean theorem, but there the ‘there
exists’ was, as I already mentioned, an abbreviation for: either p + 1 or p + 2 or p + 3 . . . or p! + 1
is a prime number — just as when, instead of saying ‘either this piece
of chalk or this piece or this piece ... or this piece is red’ we
say briefly ‘there exists a red piece of chalk among these pieces’.
A statement such as ‘there exists’ an object with a certain property
in a finite totality conforms perfectly to our finitary approach.
But a statement like ‘either p + 1 or p + 2 or p + 3 . . . or (ad infinitum) . . . has a certain property’
is itself an infinite logical product. Such an extension into the
infinite is, unless further explanation and precautions are forthcoming,
no more permissible than the extension from finite to infinite products
in calculus. Such extensions, accordingly, usually lapse into meaninglessness.
|
—
Sayılar Ve Varoluş Sorunu |
| 42. Sonlu bakış açımızdan ‘‘belli bir özelliği olan bir sayı vardır’’
biçimindeki varoluşsal bildirim genel olarak yalnızca bölümsel bir bildirimin
imlemini taşır; e.d. daha belirli bir bildirimin bir bölümü olarak görülür.
Bununla birlikte, daha sağın formülasyon birçok amaç için gereksiz olabilir. |
42. From our finitary point of view, an existential statement of the form ‘there
exists a number with a certain property’, has in general only the significance
of a partial statement; i.e., it is regarded as part of a more determinate
statement. The more precise formulation may, however, be unnecessary for
many purposes. |
| 43. İçeriği sonlu bir ayırma (disjunction) yoluyla anlatılamayan
bir varoluşsal bildirimi çözümlerken sonsuz ile karşılaşırız. Benzer olarak,
bir genel bildirimi, e.d. keyfi sayısal simgelere göndermede bulunan bir
bildirimi olumsuzlayarak bir sonluötesi bildirim elde ederiz. Örneğin
eğer a bir sayısal simge ise, o zaman a + 1 = 1 + a evrensel olarak doğrudur bildirimi sonlu perspektifimizden olumsuzlanmaya
yeteneksizdir. Eğer bu bildirimin sonsuz çoklukta sayısal eşitliğin
‘‘ve’’ aracılığıyla bir bağlanması (conjunction) olarak değil,
ama yalnızca sayısal bir simge verildiğinde birşeyi durum olarak ileri
süren bir hipotetik yargı olarak yorumlanabileceğini düşünürsek, bunu
daha iyi görürüz. |
43. In analyzing an existential statement whose content cannot be expressed
by a finite disjunction, we encounter the infinite. Similarly, by negating
a general statement, i.e., one which refers to arbitrary numerical symbols,
we obtain a transfinite statement. For example, the statement that if a is a numerical symbol, then a + 1 = 1 + a is universally
true, is from our finitary perspective incapable of negation. We
will see this better if we consider that this statement cannot be interpreted
as a conjunction of infinitely many numerical equations by means of ‘and’
but only as a hypothetical judgment which asserts something for the case
when a numerical symbol is given. |
| 44. Öyleyse, sonlu bakış açımızdan tam şimdi verilmiş olan gibi keyfi bir
sayısal simge içeren bir eşitliğin ya her simge için geçerli olduğunu
ya da bir karşı örnek tarafından çürütüldüğünü ileri süremeyiz. Böyle
bir uslamlama, dışlanmış orta yasasının bir uygulaması olmakla, böyle
bir eşitliğin evrensel geçerliğine ilişkin bildirimin yadsınmaya açık
olduğu sayıltısı üzerine dayanır. |
44.From
our finitary viewpoint, therefore, we cannot argue that an equation like
the one just given, where an arbitrary numerical symbol occurs, either holds
for every symbol or is disproved by a counter example. Such an argument,
being an application of the law of excluded middle, rests on the presupposition
that the statement of the universal validity of such an equation is capable
of negation. |
| 45. Her ne olursa olsun, şunu belirtiyoruz: Eğer sonlu bildirimler alanı
içerisinde kalırsak, ki aslında kalmalıyız, bir kural olarak önümüzde çok
karışık mantıksal yasalar bulunur. ‘‘Tüm’’ ve ‘‘vardır’’ anlatımları bileştirildiği
zaman ve başka anlatımlar içerisine yerleştirilen anlatımlar içinde yer aldıkları
zaman, sonlu bildirimlerin karmaşıklıkları denetlenemez olur. Kısaca, Aristoteles'in öğrettiği ve insanların
düşünmeye başladıkları günden bu yana kullandıkları mantıksal
yasalar geçerli değildir. Hiç kuşkusuz sonlu bildirimler alanı
için geçerli olan mantıksal yasalar geliştirebilirdik. Böyle bir mantık
geliştirmenin bize hiçbir yararı olmazdı, çünkü Aristoteles mantığının yalın
yasalarını kullanmaktan vazgeçmeyi istemiyoruz. Dahası, hiç kimse, üstelik
meleklerin dilinde bile konuşsa, insanların genel bildirimleri yadsınmalarının
ya da bölümsel yargılar oluşturmalarının ya da tertium non daturu
kullanmalarının önüne geçemezdi. O zaman ne yapacağız? |
45. At any rate, we note the following: if we remain within the domain of
finitary statements, as indeed we must, we have as a rule very complicated
logical laws. Their complexity becomes unmanageable when the expressions
‘all’ and ‘there exists’ are combined and when they occur in expressions
nested within other expressions. In short, the logical laws which Aristotle
taught and which men have used ever since they began to think, do not hold.
We could, of course, develop logical laws which do hold for the domain of
finitary statements. But it would do us no good to develop such a logic,
for we do not want to give up the use of the simple laws of Aristotelian
logic. Furthermore, no one, though he speak with the tongues of angels,
could keep people from negating general statements, or from forming partial
judgments, or from using tertium non datur. What, then, are we to
do? |
|
46. Matematikçiler
olduğumuzu ve matematikçiler olarak sık sık güvenilmez durumlarda
bulunduğumuzu ve bunlardan dahice ideal öğeler yöntemi tarafından
kurtarıldığımızı anımsayalım. Size bu denemenin başında bu yöntemin
kullanımının kimi ünlü örneklerini gösterdim. Tıpkı i = Ö-1
in cebir yasalarını en yalın biçimde saklamak için getirilmiş olması
gibi (örneğin, bir eşitliğin köklerinin varoluş ve sayısına ilişkin
yasalar); tıpkı ideal etmenlerin cebirsel tam sayılar için yalın bölünebilirlik
yasalarını saklamak için getirilmiş olması gibi (örneğin, 2 ve 1 + Ö-5 sayıları için bir ortak ideal bölen
getirildi, üstelik böyle bir bölenin gerçekten varolmamasına karşın);
benzer olarak, sıradan Aristoteles mantığının yalın biçimsel kurallarını
saklamak için, sonlu bildirimleri ideal bildirimler ile tamamlamalıyız. Kronecker’in öylesine sert olarak saldırdığı tümdengelimci
yöntemlerin Kronecker’in kendisinin Kummer’in sayı kuramı üzerine
çalışmasında (ki bunu Kronecker matematiğin en yüksek başarımı olarak
yüceltmiştir) öylesine coşkuyla hayran olduğu şeyin sağın karşıeşi
olması oldukça ironiktir.
|
46. Let us
remember that we are mathematicians and that as mathematicians we have
often been in precarious situations from which we have been rescued by
the ingenious method of ideal elements. I showed you some illustrious
examples of the use of this method at the beginning of this paper. Just
as i = Ö-1 was introduced to preserve
in simplest form the laws of algebra (for example, the laws about the
existence and number of the roots of an equation); just as ideal factors
were introduced to preserve the simple laws of divisibility for algebraic
whole numbers (for example, a common ideal divisor for the numbers 2 and
1 + Ö-5 was introduced, though no such divisor
really exists); similarly, to preserve the simple formal rules of ordinary
Aristotelian logic, we must supplement the finitary statements with
ideal statements. It is quite ironic that the deductive methods which
Kronecker so vehemently attacked are the exact counterpart of what Kronecker
himself admired so enthusiastically in Kummer’s work on number theory
which Kronecker extolled as the highest achievement of mathematics. |
| 47. İdeal bildirimleri nasıl elde ederiz? İdeal bildirimleri
elde etmek için yalnızca matematiğin temellerine ilişkin kuramda şimdiden
elde edilen gelişimi doğal ve açık bir yolda sürdürmeye gereksinim duymamız
uygun ve umutlandırıcı olduğu denli de dikkate değer bir olgudur. Aslında,
giderek öğesel matematiğin bile sezgisel sayı kuramının ötesine gittiğini
anlamalıyız. Sezgisel, özdeksel sayı kuramı, onu yorumladığımız biçimiyle,
harflerle cebirsel hesaplama yöntemini içermez. Formüller her zaman yalnızca
ve yalnızca sezgisel sayı kuramında iletişim için kullanıldılar. Harfler
sayısal simgeleri temsil ediyor ve bir eşitlik iki simgenin düşümdeştiği
olgusunu iletiyordu. Öte yandan, cebirde harfler kapsayan anlatımları
sayı kuramının özdeksel teoremlerini biçimselleştiren bağımsız yapılar
olarak görürüz. Sayısal simgelere ilişkin bildirimler yerine, kendileri
sezgisel incelemenin somut nesneleri olan formüllerimiz vardır. Sayı-kuramsal
özdeksel tanıtlama yerine, önümüzde bir formülün belirli kurallara göre
bir başkasından türetilmesi vardır. |
47. How
do we obtain ideal statements? It is a remarkable as well as a
favorable and promising fact that to obtain ideal statements, we need
only continue in a natural and obvious fashion the development which the
theory of the foundations of mathematics has already undergone. Indeed,
we should realize that even elementary mathematics goes beyond the standpoint
of intuitive number theory. Intuitive, material number theory, as we have
been construing it, does not include the method of algebraic computation
with letters. Formulas were always used exclusively for communication
in intuitive number theory. The letters stood for numerical symbols and
an equation communicated the fact that the two symbols coincided. ln algebra,
on the other hand, we regard expressions containing letters as independent
structures which formalize the material theorems of number theory. In
place of statements about numerical symbols, we have formulas which are
themselves the concrete objects of intuitive study. In place of number-theoretic
material proof, we have the derivation of a formula from another formula
according to determinate rules.
|
48. Bu
nedenle, giderek cebirde bile sonlu nesnelerin bir çoğalmasının yer
aldığını görürüz. Şimdiye dek biricik nesneler I, I I, . . ., I I I I I gibi sayısal simgelerdi. Yalnızca
bunlar özdeksel irdelemenin nesneleri idiler. Ama matematiksel kılgı
daha ileri gider, üstelik cebirde bile. Aslında, sonlu bakış açımızdan
bile bir formül simgelediği şey açısından geçerlidir, örneğin her
zaman
a + b = b + a,
teoremi gibi — ki
burada a ve b tikel sayısal simgeleri temsil etseler de,
bu iletişim biçimini kullanmamayı ama onu şu formül ile değiştirmeyi yeğleriz:
a + b = b + a,
Bu son formül hiçbir biçimde imlenen birşeyin dolaysız bir iletimi değil
ama dahaçok belli bir biçimsel yapıdır ki
2 + 3 = 3 + 2,
5 + 7 = 7
+ 5
gibi
eski sonlu bildirimler ile ilişkisi a ve b formülde
2, 3, 5, 7 gibi sayısal simgeler ile değiştirildiği zaman, böylelikle,
e.d. bir tanıtlama yordamı, ama gene de çok yalın bir yordam yoluyla
bireysel sonlu bildirimlerin elde edilmesi olgusundan oluşur. Buna
göre a, b, =, +, ve ayrıca bütün a + b = b + a formülünün,
tıpkı sayısal simgelerin herhangi birşey demek olmamaları gibi, kendilerinde
hiçbirşey demek olmadıkları vargısını çıkarırız. Gene de bu formülden
kendilerine anlam yüklediğimiz başka formüller türetebilir, ve bunu
onları sonlu bildirimlerin iletimleri olarak yorumlayarak yapabiliriz.
Bu vargıyı genelleştirerek, matematiği iki tür formüller için bir depo
olarak tasarlarız: birincisi, kendilerine sonlu bildirimlerin anlamlı
iletimlerinin karşılık düştüğü formüller; ve, ikincisi, hiçbirşey imlemeyen
ve kuramımızın ideal yapıları olan başka formüller.
|
48. Hence, as we see even in algebra, a proliferation of finitary
objects takes place. Up to now the only objects were numerical symbols like I, I I, . . ., I I I I I. These alone
were the objects of material treatment. But mathematical practice goes further,
even in algebra. Indeed, even when from our finitary viewpoint a formula
is valid with respect to what it signifies as, for example, the theorem
that always
a + b = b + a,
where a and b stand for particular numerical symbols, nevertheless we prefer
not to use this form of communication but to replace it instead by the
formula
a + b = b + a,
This
latter formula is in no wise an immediate communication of something signified
but is rather a certain formal structure whose relation to the old finitary
statements,
2 + 3 = 3 + 2,
5 + 7 = 7 + 5,
consists in the fact that, when a and b are replaced
in the formula by the numerical symbols 2, 3, 5, 7, the individual
finitary statements are thereby obtained, i.e., by a proof procedure,
albeit a very simple one. We therefore conclude that a, b,
=, +, as well as the whole formula a + b = b + a mean
nothing in themselves, no more than the numerical symbols meant
anything. Still we can derive from that formula other formulas to
which we do ascribe meaning, viz., by interpreting them as communications
of finitary statements. Generalizing this conclusion, we conceive
mathematics to be a stock of two kinds of formulas: first, those
to which the meaningful communications of finitary statements correspond;
and, secondly, other formulas which signify nothing and which are
the ideal structures of our theory.
|
49. Şimdi
amacımız neydi? Bir yanda, matematikte yalnızca sayısal simgeler kapsayan
sonlu bildirimler buluruz, örneğin
3
> 2, 2 + 3 = 3 + 2, 2 = 3, 1 ¹ 1,
ki sonlu duruş
noktamızdan başka herhangi birşeye başvurmaksızın dolaysızca sezilebilir
ve anlaşılabilirdir. Bu bildirimler doğru ya da yanlış olarak yadsınabilir.
Özel önlemler alınmaksızın Aristoteles mantığı onlara sınırsızca uygulanabilir.
Çelişmeme ilkesi onlar için geçerlidir; e.d., bu bildirimlerden birinin
yadsınması ve bildirimin kendisi ikisi birden doğru olamaz. Tertium
non datur onlar için geçerlidir; e.d., ya bir bildirim ya
da yadsınması doğrudur. Bir bildirim yanlıştır demek yadsınması doğrudur
demeye eşdeğerdir. Öte yandan, hiçbir sorun yaratmayan bu öğesel bildirimlere
ek olarak, ayrıca daha sorunlu sonlu bildirimler de buluruz; örneğin,
bölümsel bildirimlere ayrılamayan sonlu bildirimler bulduk. Son
olarak, sıradan mantık yasalarının evrensel olarak geçerli olabilmeleri
için ideal bildirimler getirdik. Ama bu ideal bildirimler, e.d. formüller
sonlu bildirimler anlatmadıkları sürece herhangi bir anlama gelmedikleri
için, mantıksal işlemler sonlu bildirimlere uygulandıkları gibi
onlara özdeksel olarak uygulanamaz. Öyleyse mantıksal işlemlerin ve
matematiksel tanıtların kendilerini biçimselleştirmek zorunludur.
Bu biçimselleştirme mantıksal ilişkileri formüllere çevirmeyi zorunlu
kılar. Bu nedenle, matematiksel simgelere ek olarak, ayrıca
& |
Ú |
® |
~2 |
(ve) |
(ya
da) |
(imler) |
(değil) |
gibi mantıksal
simgeler de getirmeliyiz, ve a, b, c, . .
. matematiksel değişkenlere ek olarak, ayrıca mantıksal değişkenler,
e.d. A, B, C, . . . gibi önermesel değişkenler
de kullanmalıyız.
2[Gerçi
Hilbert’in özgün denemesi olumsuzlama imi olarak ‘—’ imini kullanmış
olsa da, bu derlemdeki başka denemelerle kullanılan notasyona daha
uygun olması için ‘~’
imini kullandık. — İng. Yayımcılar.]
|
49. Now what was our goal? In mathematics, on the one hand, we found finitary
statements which contained only numerical symbols, for example,
3 > 2, 2 + 3 = 3 + 2, 2 = 3, 1 ¹ 1,
which from our
finitary standpoint are immediately intuitable and understandable without
recourse to anything else. These statements can be negated, truly or
falsely. One can apply Aristotelian logic unrestrictedly to them without
taking special precautions. The principle of non-contradiction holds
for them; i.e., the negation of one of these statements and the statement
itself cannot both be true. Tertium non datur holds for them;
i.e., either a statement or its negation is true. To say that a statement
is false is equivalent to saying that its negation is true. On the other
hand, in addition to these elementary statements which present no problems,
we also found more problematic finitary statements; e.g., we found finitary
statements that could not be split up into partial statements. Finally,
we introduced ideal statements in order that the ordinary laws of logic
would hold universally. But since these ideal statements, viz., the
formulas, do not mean anything insofar as they do not express finitary
statements, logical operations cannot be materially applied to them
as they can be to finitary statements. It is, therefore, necessary to
formalize the logical operations and the mathematical proofs themselves.
This formalization necessitates translating logical relations into formulas.
Hence, in addition to mathematical symbols, we must also introduce logical
symbols such as
& |
Ú |
® |
~2 |
(and) |
(or) |
(implies) |
(not) |
and in addition
to the mathematical variables a, b, c, . . . we must also employ logical variables, viz., the propositional variables A, B, C, . . . .
2[Although
Hilbert’s original paper used ‘—’ as the sign for negation, we have
substituted ‘~’
for greater conformity with the notation used in other papers in this
collection. — Eds.].
|
50. Bu nasıl yapılabilir? Ne sevindiricidir ki, bilimin
gelişiminin tarihinde öylesine sık gözlemiş olduğumuz o aynı önceden-saptanmış
uyum, Einstein’a onun yerçekimi kuramı için daha şimdiden tam olarak gelişmiş
genel değişmesizlik kalkülüsü vermekle yardım eden o aynı önceden-saptanmış
uyum bizim yardımımıza da gelir: mantıksal kalkülüsün önceden geliştirilmiş
olduğunu buluruz. Hiç kuşkusuz, mantıksal kalkülüs başlangıçta bütünüyle
ayrı bir bakış açısından geliştirildi. Mantıksal kalkülüsün simgeleri
başlangıçta yalnızca iletişimde bulunabilmek için getirildiler. Gene de
mantıksal simgelere herhangi bir anlamı yadsımak — tıpkı matematiksel
simgelerin anlamını yadsımış olmamız gibi —, ve matematiksel kalkülüsün
formüllerinin kendilerinde hiçbir anlamı olmayan ideal bildirimler olduklarını
bildirmek bizim sonlu bakış açımızdan tutarlıdır. Mantıksal kalkülüste
simgesel bir dil buluruz ki matematiksel bildirimleri formüllere dönüştürebilir
ve biçimsel yordamlar aracılığıyla mantıksal tümdengelimi anlatabilir. Özdeksel
sayı kuramından biçimsel cebire geçiş ile sağın andırım içinde, şimdi
mantıksal kalkülüsün imlerini ve işlem simgelerini anlamlarından soyutlama
içinde kullanırız. Böylece sonunda, sıradan dilde iletilen özdeksel matematiksel
bilgi yerine, tam olarak belirli kurallara göre ardışık olarak üretilmiş
matematiksel ve mantıksal simgeler kapsayan bir formüller kümesi elde
ederiz. Formüllerden kimileri matematiksel belitlere karşılık düşer. Formüllerin
birbirinden türetilmesini sağlayan kurallar özdeksel tümdengelime karşılık
düşer. Özdeksel tümdengelim böylece kurallar tarafından yönetilen bir biçimsel
yordam ile değiştirilir. Saf bir irdelemeden biçimsel bir irdelemeye sağın
geçiş, buna göre, hem belitler için (ki, başlangıçta safça temel gerçeklikler
olarak görülmelerine karşın, çoktandır modern belit kuramında salt kavramlar
arasındaki ilişkiler olarak ele alınırlar) hem de mantıksal kalkülüs için
(ki başlangıçta salt değişik bir dil olması gerekiyordu) yerine getirilir. |
50. How can this be done? Fortunately that same preestablished
harmony which we have so often observed operative in the history of the
development of science, that same preestablished harmony which aided Einstein
by giving him the general invariant calculus already fully developed for
his gravitational theory, comes also to our aid: we find the logical calculus
already worked out in advance. To be sure, the logical calculus was originally
developed from an altogether different point of view. The symbols of the
logical calculus originally were introduced only in order to communicate.
Still it is consistent with our finitary viewpoint to deny any meaning to
logical symbols, just as we denied meaning to mathematical symbols, and
to declare that the formulas of the logical calculus are ideal statements
which mean nothing in themselves. We possess in the logical calculus a symbolic
language which can transform mathematical statements into formulas and express
logical deduction by means of formal procedures. In exact analogy to the
transition from material number theory to formal algebra, we now treat the
signs and operation symbols of the logical calculus in abstraction from
their meaning. Thus we finally obtain, instead of material mathematical
knowledge which is communicated in ordinary language, just a set of formulas
containing mathematical and logical symbols which are generated successively,
according to determinate rules. Certain of the formulas correspond to mathematical
axioms. The rules whereby the formulas are derived from one another correspond
to material deduction. Material deduction is thus replaced by a formal procedure
governed by rules. The rigorous transition from a naive to a formal treatment
is effected, therefore, both for the axioms (which, though originally viewed
naively as basic truths, have been long treated in modern axiomatics as
mere relations between concepts) and for the logical calculus (which originally
was supposed to be merely a different language). |
51. Şimdi
kısaca matematiksel tanıtların nasıl biçimselleştirildiklerini
açıklayacağız. Daha önce matematiğin biçimsel yapısı için yapı taşları
olarak hizmet eden belli formüllere ‘‘belitler’’ dendiğini söylemiştim.
Bir matematiksel tanıt sezgimize
açık olması gereken türde bir betidir. Şu tümdengelim şemasına göre
yapılan tümdengelimlerden oluşur

ki burada her bir öncül, e.d.  ve ve  ® ®  formülleri,
ya bir belittir, ya da yerdeğiştirme yoluyla bir belitten doğar,
ya da bir önceki tümdengelimin son formülüdür, ya da yerdeğiştirme
yoluyla böyle bir formülden doğar. Bir formülün eğer bir tanıtın
son formülü ise tanıtlanabilir olduğu söylenir. formülleri,
ya bir belittir, ya da yerdeğiştirme yoluyla bir belitten doğar,
ya da bir önceki tümdengelimin son formülüdür, ya da yerdeğiştirme
yoluyla böyle bir formülden doğar. Bir formülün eğer bir tanıtın
son formülü ise tanıtlanabilir olduğu söylenir.
|
51. We
will now explain briefly how mathematical proofs are formalized.
I have already said that certain formulas which serve as building blocks
for the formal structure of mathematics are called ‘‘axioms’’. A mathematical
proof is a figure which as such must be accessible to our intuition. It
consists of deductions made according to the deduction schema
where each premise,
i.e., the formulas  and and  ® ® ,
either is an axiom, or results from an axiom by substitution, or is the
last formula of a previous deduction, or results from such a formula by
substitution. A formula is said to be provable if it is the last formula
of a proof. ,
either is an axiom, or results from an axiom by substitution, or is the
last formula of a previous deduction, or results from such a formula by
substitution. A formula is said to be provable if it is the last formula
of a proof. |
52. İzlencemizin kendisi tanıtlama kuramı için belitlerin seçimine yol gösterir. Belitlerin seçiminde belli bir
keyfilik miktarına karşın, geometride olduğu gibi belli belit
kümeleri nitel olarak ayırdedilemezdir. Bu kümelerden alınan kimi örnekler şunlardır:
I. İmlem belitleri
(i) A ® (B ® A)
(bir hipotezin eklenmesi)
(ii) (B ® C) ® {(A ® B) ® (A ® C)}
(bir bildirimin ortadan kaldırılması)
II. Olumsuzlama
belitleri
(i)
{A ® (B & ~B)} ® ~A
(çelişki yasası)
(ii) ~~A ® A
(çifte olumsuzlama yasası)
I ve II. kümelerdeki
belitler yalnızca önerme kalkülüsünün belitleridirler.
III. Sonluötesi belitler
(i) (a)A(a) ® A(b)
(evrenselden tikele çıkarsama; Aristoteles beliti);
(ii) ~(a)A(a) ® ($a)~A(a)
(eğer bir yüklem evrensel olarak geçerli değilse, o zaman bir karşı-örnek
vardır);
(iii) ~($a)A(a) ® (a)~A(a)
(eğer bir önermenin hiçbir örneği yoksa, o zaman önerme tüm a için yanlıştır).
Bu noktada bu sonluötesi
belitlerin seçim beliti denilen ve matematik yazınında en çok tartışılan
belitin özünü kapsayan tek bir belitten türetilebileceği biçimindeki
çok dikkate değer olguyu keşfederiz:
(i¢) A(a) ® A(eA)
ki
burada e sonluötesi, mantıksal seçim-işlevidir.
Sonra aşağıdaki özel olarak matematiksel belitler tam şimdi verilenlere
eklenir:
IV. Özdeşlik için belitler
(i) a = a
(ii) a = b ® {A(a) ® A (b)},
V.
Sayı için belitler
(i) a + 1 ¹ 0
(ii) Tam tümevarım beliti.
|
52. Our program
itself guides the choice of axioms for our theory of proof. Notwithstanding
a certain amount of arbitrariness in the choice of axioms, as in geometry
certain groups of axioms are qualitatively distinguishable. Here are some
examples taken from each of these groups:
I. Axioms for implication
(i) A ® (B ® A)
(addition of a hypothesis)
(ii) (B ® C) ® {(A ® B) ® (A ® C)}
(elimination of a statement)
II. Axioms for negation
(i) {A ® (B & ~B)} ® ~A
(law of contradiction)
(ii) ~~A ® A
(law of double negation)
The axioms in groups
I and II are simply the axioms of the propositional calculus.
III. Transfinite
axioms
(i) (a)A(a) ® A(b)
(inference from the universal to the particular; Aristotelian axiom);
(ii) ~(a)A(a) ® ($a)~A(a)
(if a predicate does not apply universally, then there is a counter-example);
(iii) ~($a)A(a) ® (a)~A(a)
(if there are no instances of a proposition, then the proposition is
false for all a).
At this point we
discover the very remarkable fact that these transfinite axioms can be
derived from a single axiom which contains the gist of the so-called axiom
of choice, the most disputed axiom in the literature of mathematics:
(i¢) A(a) ® A(eA)
where e is the transfinite, logical choice-function.
Then the following specifically mathematical axioms are added to those
just given:
IV. Axioms for identity
(i) a = a
(ii) a = b ® {A(a) ® A (b)},
and finally
V. Axioms for number
(i) a +
1 ¹ 0
(ii) The axiom of complete induction.
|
—
Belitlerin Seçiminde Belli Bir Keyfilik Miktarı Vardır
[Yoktur.
Belitlerin
keyfiliği onların üzerine kurulan teoremin de keyfiliğidir. Ama geometrik
teorem ussal ise, niceliğin kavramsal davranışını anlatıyorsa, aynı ussallığa
özdeksel niceliğin, uzaysal ve zamansal niceliğin de yanıt vermemesi bu
son kavramların usdışı oldukları, birer kavram olmadıkları anlamına gelir.
Gerçekten de görgücülük bu kavramların kendilerinde varlıklarını, mantıksal
varlıklarını yadsır. Algıdan hiçbir gerçeklik türetilemez.] |
53. Böylece şimdi tanıtlama kuramını yerine getirecek ve tanıtlanabilir
formüller dizgesini, e.d. matematiği kurabilecek bir konumdayız. Ama bu
başarım üzerine genel sevincimizde ve bu vazgeçilmez aleti, bizim payımıza
herhangi bir çaba olmaksızın daha şimdiden geliştirilmiş mantıksal kalkülüsü
bulma üzerine özel sevincimizde, çalışmamızın özsel koşulunu unutmamalıyız.
Tek bir koşul, ama gene de ideal öğeler yöntemi ile bağıntılı saltık olarak
zorunlu bir koşul daha vardır. Bu koşul bir tutarlılık tanıtıdır, çünkü
bir alanın ideal öğelerin eklenmesiyle genişletilmesi ancak genişleme
eski ve daha dar alanda çelişkilerin doğmasına neden olmazsa, ya da, başka
bir deyişle, ancak ideal yapılar silindiği zaman eski yapılar arasında
geçerli olan ilişkiler her zaman eski alanda geçerli iseler meşrudur. |
53. Thus we are now in a position to carry out our theory of proof and to
construct the system of provable formulas, i.e., mathematics. But in our
general joy over this achievement and in our particular joy over finding
that indispensable tool, the logical calculus, already developed without
any effort on our part, we must not forget the essential condition of our
work. There is just one condition, albeit an absolutely necessary one, connected
with the method of ideal elements. That condition is a proof of consistency,
for the extension of a domain by the addition of ideal elements is legitimate
only if the extension does not cause contradictions to appear in the old,
narrower domain, or, in other words, only if the relations that obtain among
the old structures when the ideal structures are deleted are always valid
in the old domain. |
54. Tutarlılık sorunu bu durumda kolayca ele alınabilir. Açıktır ki belitlerimizden,
ve ortaya koyduğumuz kurallara göre, ‘1 ¹ 1’i
bir tanıtlamanın son formülü olarak bulamadığımızı, başka bir deyişle,
‘1 ¹ 1’in tanıtlanabilir bir formül olmadığını
tanıtlamaya indirgenir. Bu görev sezgisel irdeleme alanına en azından
özdeksel olarak kurulu sayı kuramında Ö2 nin
kesirsizliğinin bir tanıtını bulma görevi denli aittir — e.d., a2 = 2b2 ilişkisinde duran a ve b gibi iki
sayısal simgeyi bulmanın olanaksızlığının, ya da başka bir deyişle, belli
bir özellikleri olan iki sayısal simgenin üretilememesinin bir tanıtını
bulma görevi gibi. Benzer olarak, üzerimize belli bir tanıtlama türünün
üretilemeyeceğini gösterme görevi de düşer. Biçimselleştirilmiş bir
tanıtlama, tıpkı sayısal bir simge gibi, somut ve görülebilir bir nesnedir. Onu tam olarak betimleyebiliriz. Dahası, son
formülün gerekli özelliği, e.d. ‘1 ¹ 1’i vermesi,
tanıtlamanın somut olarak saptanabilir bir özelliğidir. Ve, gerçekten
de, bu formülü son formülü olarak almayan bir tanıtlama bulmanın olanaksız
olduğunu tanıtlayabileceğimize göre, böylelikle ideal bildirimleri getirişimizi
aklamış oluruz |
54. The problem of consistency is easily handled in the present circumstances.
It reduces obviously to proving that from our axioms and according to the
rules we laid down we cannot get ‘1 ¹ 1’ as
the last formula of a proof, or, in other words, that ‘1 ¹ 1’ is not a provable formula. This task belongs just as much to
the domain of intuitive treatment as does, for example, the task of finding
a proof of the irrationality of Ö2 in materially
constructed number theory — i.e., a proof that it is impossible to find
two numerical symbols a and b which stand in the relation a2 = 2b2, or in other words, that one
cannot produce two numerical symbols with a certain property. Similarly,
it is incumbent on us to show that one cannot produce a certain kind of
proof. A formalized proof, like a numerical symbol, is a concrete and visible
object. We can describe it completely. Further, the requisite property of
the last formula; viz., that it read ‘1 ¹ 1’,
is a concretely ascertainable property of the proof. And since we can, as
a matter of fact, prove that it is impossible to get a proof which has that
formula as its last formula, we thereby justify our introduction of ideal
statements. |
55. Ayrıca
tam olarak aynı zamanda matematikçileri uzun bir süredir uğraştıran
bir sorunu, e.d. aritmetiğin belitlerinin tutarlığını tanıtlama sorununu
çözmüş olduğumuzu keşfetmemiz de hoş bir sürprizdir.
Çünkü, nerede belit yöntemi kullanılsa, tutarlığı tanıtlama sorunu doğar.
Hiç kuşkusuz kuralları ve belitleri seçmede, anlamada ve kullanmada
yalnızca kör inanca güvenmeyi istemeyiz. Geometride ve fiziksel kuramda
tutarlılık tanıtı onların tutarlıklarını aritmetiğin belitlerinin tutarlığına
indirgeme yoluyla ortaya çıkarılır. Ama açıktır ki bu yöntemi aritmetiğin
kendisinin tutarlığını tanıtlamak için kullanamayız. İdeal öğeler yöntemi
üzerine dayalı tanıtlama kuramımız bize bu son adımı atma olanağını
verdiği için, belit kuramının öğretisel kemerlerinden birinin zorunlu
anahtar taşını oluşturur. Bir kez sonsuz küçüklük kalkülüsünün paradoksları
ile ve bir kez de küme kuramının paradoksları ile iki kez yaşadığımız
şey bir üçüncü kez daha yaşanmayacak, bir daha hiç yaşanmayacaktır.
|
55. It is also a pleasant surprise to discover that, at the very same time,
we have resolved a problem which has plagued mathematicians for a long time,
viz., the problem of proving the consistency of the axioms of arithmetic.
For, wherever the axiomatic method is used, the problem of proving consistency
arises. Surely in choosing, understanding, and using rules and axioms we
do not want to rely solely on blind faith. In geometry and physical theory,
proof of consistency is effected by reducing their consistency to that of
the axioms of arithmetic. But obviously we cannot use this method to prove
the consistency of arithmetic itself. Since our theory of proof, based on
the method of ideal elements, enables us to take this last important step,
it forms the necessary keystone of the doctrinal arch of axiomatics. What
we have twice experienced, once with the paradoxes of the infinitesimal
calculus and once with the paradoxes of set theory, will not be experienced
a third time, nor ever again. |
56. Burada taslağını verdiğimiz tanıtlama kuramı yalnızca matematiğin
temelleri için sağlam bir dayanak sağlayabilmekle kalmaz, ama, inanıyorum
ki, ayrıca matematikçilerin şimdiye dek ele almayı başaramadıkları temel
matematiksel soruları irdelemek için genel bir yöntem de sağlar. |
56. The theory of proof which we have here sketched not only is capable
of providing a solid basis for the foundations of mathematics but also,
I believe, supplies a general method for treating fundamental mathematical
questions which mathematicians heretofore have been unable to handle. |
57. Bir anlamda matematik temel sorular üzerine karar vermek için ve
bunu üzerinde herkesin anlaşabileceği ve her bildirimin denetlenebileceği
somut bir temel üzerinde yapmak için bir hakemlik mahkemesi, bir yüksek
mahkeme olmuştur.
|
57. In a sense,
mathematics has become a court of arbitration, a supreme tribunal to decide
fundamental questions — on a concrete basis on which everyone can agree
and where every statement can be controlled. |
58. ‘‘Sezgicilik’’
denilen yeni çizginin önerüsümleri, ne denli alçakgönüllü olsalar da,
benim görüşümde ilkin geçerlik yetkilerini bu mahkemeden almalıdırlar.
|
58. The
assertions of the new so-called ‘‘intuitionism’’ — modest though they
may be — must in my opinion first receive their certificate of validity
from this tribunal. |
59. ‘‘Sezgicilik’’ denilen yeni çizginin önerüsümleri, ne denli alçakgönüllü
olsalar da, benim görüşümde ilkin geçerlik yetkilerini bu mahkemeden almalıdırlar. |
59. The assertions of the new so-called ‘‘intuitionism’’ — modest though they
may be — must in my opinion first receive their certificate of validity
from this tribunal. |
60. Böyle ele alınabilecek türde temel soruların bir örneği her matematiksel
problemin çözülebilir olduğu savıdır. Hepimiz bunun gerçekten böyle olduğu
kanısındayız. Gerçekte bir matematiksel problem ile uğraşmanın en çekici
yanlarından biri şu çığlığı içimizde her zaman duymamızdır: Problem burada,
yanıtı bul: onu yalnızca düşünerek bulabilirsin, çünkü matematikte bilinemeyecek
hiçbirşey yoktur. Şimdi benim tanıtlama kuramım her matematiksel problemin
çözümü için genel bir yöntem sunamaz — böyle bir yöntem kesinlikle yoktur.
Gene de tanıtlama (her matematiksel problemin çözülebilir olduğu sayıltısı
tutarlı bir sayıltıdır) tam olarak kuramımızın alanı içerisine düşer.* |
60. An example of the kind of fundamental questions which can be so handled
is the thesis that every mathematical problem is solvable. We are all convinced
that it really is so. In fact one of the principal attractions of tackling
a mathematical problem is that we always hear this cry within us: There
is the problem, find the answer; you can find it just by thinking, for there
is no ignorabimus in mathematics. Now my theory of proof cannot supply
a general method for solving every mathematical problem-there just is no
such method. Still the proof (that the assumption that every mathematical
problem is solvable is a consistent assumption) falls completely within
the scope of our theory. |
—
Her Matematiksel Problem Çözülebilir Mi?
*[Bu
sayıltı yalnızca matematiğin kendi içinde bütünüyle tutarlı, uyumlu ya
da ussal bir yapı olduğunu değil, ama matematik ve olgusallık arasında
nicelik açısından bütünüyle tutarlı bir ilişki olduğunu da imlemelidir.
Hilbert’in tüm çabasına karşın, matematiksel tanıtlamanın ya da uslamlamanın
doğası hiçbir duruluk kazanmış değildir. Nicelik kavramının eytişimini
dikkate almamak bu kavramın kendisini dikkate almamak, onu yalnızca doğal
usun işlevinde kullanmaktır. Ancak kavram — süreklilik ve kesiklilik —
bir yana atılaraktır ki ‘bir aralıktaki noktalar ‘sayılabilir.’
Gene de problemler çözülür, çünkü doğal usun işlevinde çözülür, ve çözümsüzlük
kuşkusu ussallık kuşkusundan başka hiçbir anlama gelmez. Matematiksel
bilinç kavramını tanımaksızın da iş görebilir, çünkü kavramın işlevi analitik
tek-yanlılık tarafından durdurulmadıkça işler. Ama Cantor başaramadı,
çünkü tek-yanlı kesikliliğin sözcülüğünü üstlendi. Bu nedenle doğal matematiksel
usa çılgınca göründü.
Felsefe
varolan herşeyin, tüm edimselliğin ussal olduğunu tanıtlamıştır, ve kavramın
sağınlığının şu ya da bu noktada çökmesi gibi bir kaygı taşımaz. Bu tanıtlama
felsefenin kendisidir ve bilinç eytişimin gerçek doğasını kavramadığı
sürece, bu sorunu çözmeksizin kuşkuculuğa sığınması için hiçbir haklı
gerekçe bulamaz. Kuşkuculuk bu anlamda da çabadan vazgeçmek, ve salt gereksiz
bir gürültü yapmaktır. Matematiksel tanıtlama, ve matematiksel tablonun
olgusallık ile ilişkisi konuları Hilbert’in dediği gibi, olağanüstü çekicidir.
Ama aynı tanıtlama ve aynı gerçeklik arayışı tarihte, törel yaşamda, doğa
biliminde, estetikte, ruhbilimde, insan varoluşunun her alanında en azından
eşit ölçüde çekicidir.] |
61. Şimdi son kozumu oynayacağım. Yeni kuramın asit testi uzun bir süredir
bilinmelerine karşın kuramın kesinlikle onları çözmek için tasarlanmadığı
problemleri çözme yeteneğidir. ‘‘Onları meyvalarından tanıyacaksınız’’
düzgüsü kuramlar için de geçerlidir. Cantor ilk sonluötesi sayılarını,
ikinci sayı sınıfının sayıları denilen şeyleri keşfettiği zaman, dolaysızca
ortaya çıkan soru, daha önce değindiğim gibi, bu sonluötesi sayma yönteminin
başka bir yerden bilinen ve olağan anlamda sayılabilir olmayan kümeleri
sayma olanağını verip vermediği sorusuydu. Bir aralığın noktaları çarpıcı
bir yolda böyle bir küme olarak ortaya çıktılar. Bu soru — bir aralığın
noktalarının, e.d. reel sayıların, daha önce verilen tablonun sayıları
aracılığıyla sayılıp sayılamayacağı sorusu — Cantor’un ortaya koyduğu
ama çözmeyi başaramadığı ünlü süreklilik problemidir. Gerçi kimi matematikçiler
bu problemin varoluşunu yadsıyarak ondan kurtulabileceklerini düşünmüş
olsalar da, şu gözlemler ne denli yanılmış olduklarını gösterir: Süreklilik
problemi başka problemlerden benzersizliği ve iç güzelliği ile ayrılır.
Dahası, öteki problemler üzerinde şu iki niteliği bileştirme üstünlüğünü
sunar: Bir yandan, çözümü için yeni yöntemler gereklidir çünkü eski yöntemler
onu çözmeyi başaramazlar; öte yandan, çözümünün kendisi elde edilecek
sonuçlardan ötürü çok önemlidir. |
61. I will
now play my last trump.
The acid test of a new theory is its ability to solve problems which,
though known for a long time, the theory was not expressly designed to
solve. The maxim ‘‘By their fruits ye shall know them’’ applies also to
theories. When Cantor discovered his first transfinite numbers, the so-called
numbers of the second number class, the question immediately arose, as
I already mentioned, whether this transfinite method of counting enables
one to count sets known from elsewhere which are not countable in the
ordinary sense. The points of an interval figured prominently as such
a set. This question — whether the points of an interval, i.e., the real
numbers, can be counted by means of the numbers of the table given previously
— is the famous continuum problem which Cantor posed but failed to solve.
Though some mathematicians have thought that they could dispose of this
problem by denying its existence, the following remarks show how wrong
they were: The continuum problem is set off from other problems by its
uniqueness and inner beauty. Further, it offers the advantage over other
problems of combining these two qualities: on the one hand, new methods
are required for its solution since the old methods fail to solve it;
on the other hand, its solution itself is of the greatest importance because
of the results to be obtained. |
62. Geliştirdiğim
kuram süreklilik probleminin bir çözümünü sağlar. Her matematiksel problemin
çözülebilir olduğunun tanıtı onun çözümüne doğru ilk ve en önemli adımı
oluşturur.3
3[Bu
noktada Hilbert süreklilik probleminin çözümü için bir girişim taslağını
verir. Girişim ilginç olsa da hiçbir zaman tamamlanmadı. Bu nedenle burada
onu atlıyoruz. — Yayımcılar]
|
62. The theory
which I have developed provides a solution of the continuum problem. The
proof that every mathematical problem is solvable constitutes the first
and most important step toward its solution.3
3[At this
point, Hilbert sketched an attempted solution of the continuum problem.
The attempt was, although not devoid of interest, never carried out. We
therefore omit it here. — Eds.] |
63. Özet olarak, ana temamıza geri dönelim ve sonsuza ilişkin tüm düşüncelerimizden
kimi vargılar çıkaralım. Başlıca sonucumuz sonsuzun
olgusallıkta hiçbir yerde bulunamayacak olduğudur. Ne doğada
vardır, ne de ussal düşünce için meşru bir temel sağlar — varlık ve düşünce
arasında dikkate değer bir uyum. Frege ve Dedekind’in daha önceki çabaları
ile karşıtlık içinde, inanıyoruz ki belli sezgisel kavramlar ve içgörüler
bilimsel bilginin zorunlu koşullarıdır, yalnızca mantık yeterli değildir.
Sonsuz ile iş görmek ancak sonluluk yoluyla pekin kılınabilir. |
63. In summary, let us return to our main theme and draw some conclusions from
all our thinking about the infinite. Our principal result is that the infinite
is nowhere to be found in reality. It neither exists in nature nor provides
a legitimate basis for rational thought — a remarkable harmony between being
and thought. In contrast to the earlier efforts of Frege and Dedekind, we
are convinced that certain intuitive concepts and insights are necessary
conditions of scientific knowledge, that logic alone is not sufficient.
Operating with the infinite can be made certain only by the finitary. |
—
Sonsuz Olgusallıkta Hiçbir Yerde Bulunmaz
— Sonsuz
İle Ancak Sonlu Olan Yoluyla İşlem Yapılabilir
[Sağın
konuşmak gerekirse, Sonsuz ancak Sonlulaştırılarak analitik anlak düzlemine
getirilebilir. Ama Sonsuzun Sonlulaştırılması anlağın bile başaramayacağı
bir el çabukluğudur. Hilbert’in matematikçiliği böyle daha yüksek gerçeklikler
üzerine, daha bilimsel sezgiler vb. üzerine dayanır. Daha da iyisi, gerçeklik,
bilimsellik gibi kavramları bir yana atmaktır. Pozitivizm sonunda bunu
yapar.] |
64. Sonsuz için geriye kalan rol yalnızca bir düşüncenin rolüdür — eğer bir
düşünce ile denmek istenen şey, Kant’ın terminolojisinde, tüm deneyimi
aşan ve bir bütünlük olarak — kuramımız tarafından çizilen çerçeve içerisinde
hiçbir duraksama göstermeden güvenebileceğimiz bir düşüncenin bütünlüğü
olarak — somutu tamamlayan bir us-kavramı ise. |
64. The role that remains for the infinite to play is solely that of an idea
— if one means by an idea, in Kant’s terminology, a concept of reason which
transcends all experience and which completes the concrete as a totality
— that of an idea which we may unhesitatingly trust within the framework
erected by our theory. |
65. Son olarak P. Bernays’a özellikle süreklilik teoreminin tanıtı ile
ilgili olarak hem uygulayımsal hem de yazınsal açıdan akıllıca işbirliği
ve değerli yardımı için teşekkür etmek istiyorum. |
65. Lastly, I wish to thank P. Bernays for his intelligent collaboration
and valuable help, both technical and editorial, especially with the proof
of the continuum theorem. |
|